
第三节三重积分三重积分的概念三重积分的计算返回MathGS公式上页下页线与面数学家
第三节 三重积分 一、三重积分的概念 二、三重积分的计算

第三节三重积分一、三重积分的概念定义设f(x,,z)是空间有界闭区域Q上的有界函数.将Q任意分成n个小闭区域△V,△,.,△V其中△v表示第i个小闭区域,也表示它的体积。在每个Av上任取一点(,ni,Si),作乘积f(,ni,Si)△vf(5,ni,S)Av.如果当各小(i=1, 2,.….,n),并作和il闭区域直径中的最大值入趋于零时这和的极限存在则称此极限为函数f(x,y,z)在区域2上的三重积分MathGS上页下页返回公式数学家线与面
第三节 三重积分 一、三重积分的概念 定义设 f (x , y , z) 是空间有界闭区域 上的有界 函数. 将 任意分成 n 个小闭区域 v1 , v2 , . , vn , 其中vi 表示第 i 个小闭区域,也表示它的体积. 在每 个vi上任取一点( i , i , i ),作乘积 f (i , i , i ) vi (i = 1, 2, . , n), 并作和 = n i i i i i f v 1 ( , , ) . 如果当各小 闭区域直径中的最大值 趋于零时这和的极限存在, 则称此极限为函数 f (x , y , z) 在区域 上的三重积分

第三节三重积分记作[J f(x, y,z)dv,Q即Ef(E,ni,S)Av,JJJ f(x, y,z)dv= lim )1-0=12其中dv叫做体积元素在直角坐标系中,体积元素dy= dxdydz三重积分也有与二重积分完全类似的性质返回MathGS公式上页下页线与面数学家
第三节 三重积分 记作 ( , , )d , Ω f x y z v 即 ( , , )d ( , , ) , 0 1 lim → = = n i i i i i Ω f x y z v f v 其中 dv 叫做体积元素. 在直角坐标系中,体积元素 dv = dxdydz . 三重积分也有与二重积分完全类似的性质

第三节三重积分三重积分的计算二、1.利用直角坐标计算三重积分(1)坐标面投影法设积分区域Q向xOy面投影区域为Dxy,且Q能够(x,y)eDy,表示为Q:zi(x,y),z2(x, y)eC(Dx)[z)(x, y)≤z≤z2(x, y),区域2的特点:任何一条垂直于x0v面且穿过Q内部的直线与Q的边界曲面相交不多于两点上页下页返回MathGS公式数学家线与面
第三节 三重积分 二、三重积分的计算 (1) 坐标面投影法 1. 利用直角坐标计算三重积分 设积分区域 向 xOy面投影区域为 Dxy ,且 能够 表示为 ( , ) ( , ) , ( , ) , : 1 2 z x y z z x y x y D Ω xy ( , ), ( , ) ( ). 1 2 C Dxy z x y z x y 区域 的特点:任何一条垂直于 xOy面且穿过 内部的 直线与 的边界曲面相交不多于两点
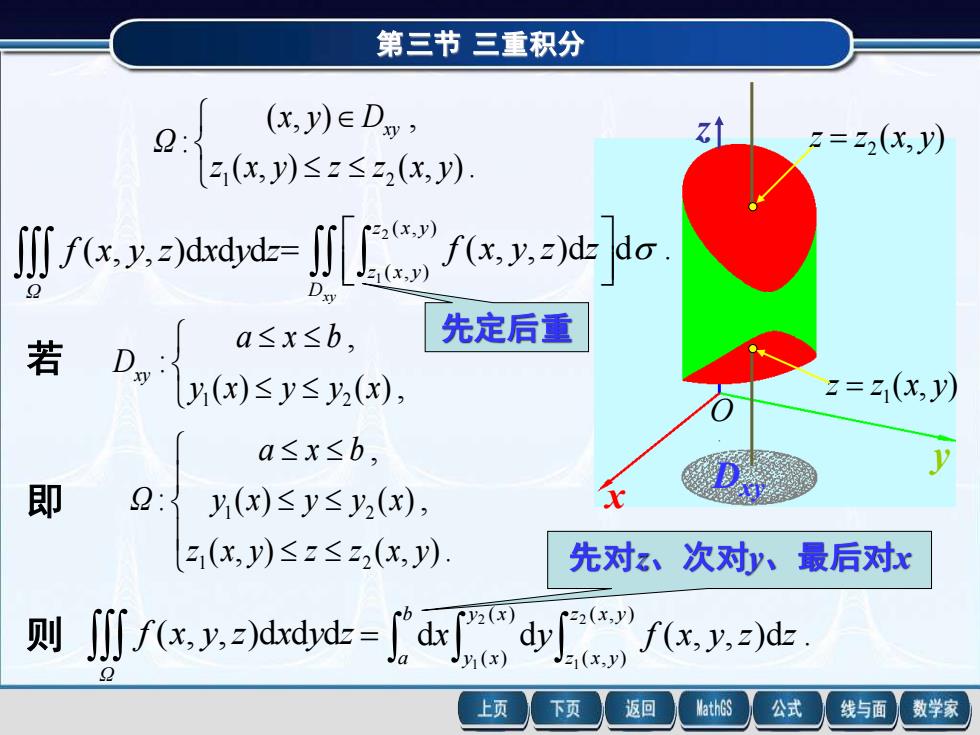
第三节三重积分(x,y)e Dy ,zTZ= 22(x, y)z(x,y)≤z≤z2(x,y)Z2(Jei([] f(x, y,z)dxdydz=f(x, y,z)dz dJzr(xy2Dsy先定后重a≤x≤b,若Dxyz= z(x,y)(yi(x)≤y≤y2(x) ,a≤x≤b,y福即x2:y(x)≤y≤y2(x),(2i(x,y)≤z≤z2(x, y).先对z、次对y、最后对xz2(x,y)则 [f f(x, y,z)dxdydz= ~ dx ]f(x, y,z)dzdyJyi(x)z1(XVQ上页下页返回MathGS公式数学家线与面
第三节 三重积分 x y z O Dxy ( , ) 2 z = z x y ( , ) 1 z = z x y ( , ) ( , ). ( , ) , : 1 2 z x y z z x y x y D Ω xy Ω f (x, y,z)dxdydz ( , , )d d . ( , ) ( , ) 2 1 = Dxy z x y z x y f x y z z 若 ( ) ( ) , , : 1 2 y x y y x a x b Dxy 则 Ω f (x, y,z)dxdydz d d ( , , )d . ( , ) ( , ) ( ) ( ) 2 1 2 1 = z x y z x y y x y x b a x y f x y z z 即 ( , ) ( , ). ( ) ( ) , , : 1 2 1 2 z x y z z x y y x y y x a x b Ω 先定后重 先对z、次对y、最后对x