
第七节傅里叶级数一、引入基本概念函数展开成傅里叶级数一四、正弦级数和余弦级数返回MathGS公式上页下页线与面数学家
第七节 傅里叶级数 二、基本概念 四、正弦级数和余弦级数 三、函数展开成傅里叶级数 一、引入

第七节傅里叶级数一、引入在第四节中,我们讨论了将函数展开成幂级数的问题,在本节中,我们将讨论周期函数展开成三角级数的问题,正弦函数是一种常见而又简单的周期函数.例如描述简谐振动的函数振幅初相角频率y= Asin(の t +@)2元就是一个以为周期的正弦函数0下页返回MathGS公式数学家上页线与面
第七节 傅里叶级数 一、引入 在第四节中,我们讨论了将函数展开成幂级数的问 题,在本节中,我们将讨论周期函数展开成三角级数的 问题. 正弦函数是一种常见而又简单的周期函数.例如描 述简谐振动的函数 y = Asin( t +) 就是一个以 2π 为周期的正弦函数. 振幅 角频率 初相

第七节傅里叶级数那么其他非正弦函数的周期函数能否由不同频率的正弦函数叠加而成呢?请看下面的例子8sin nx>利用工具箱中的无例1设有函数项级数nn=l穷级数工具,研究(1)部分和Sk(x)是不是周期函数;(2)部分和Sk(x)的连续性:(3)部分和数列s(x)是否收敛MathGS上页下页返回公式线与面数学家
第七节 傅里叶级数 那么其他非正弦函数的周期函数能否由不同频率的 正弦函数叠加而成呢? 请看下面的例子. 例1 设有函数项级数 , sin 1 n= n nx 利用工具箱中的无 穷级数工具,研究 (1) 部分和 sk (x) 是不是周期函数; (2) 部分和 sk (x) 的连续性; (3) 部分和数列 sk (x) 是否收敛
第七节傅里叶级数解部分和的图形前1项和前3项和前6项和前16项和前60项和前260项和返回MathGS公式上页下页线与面数学家
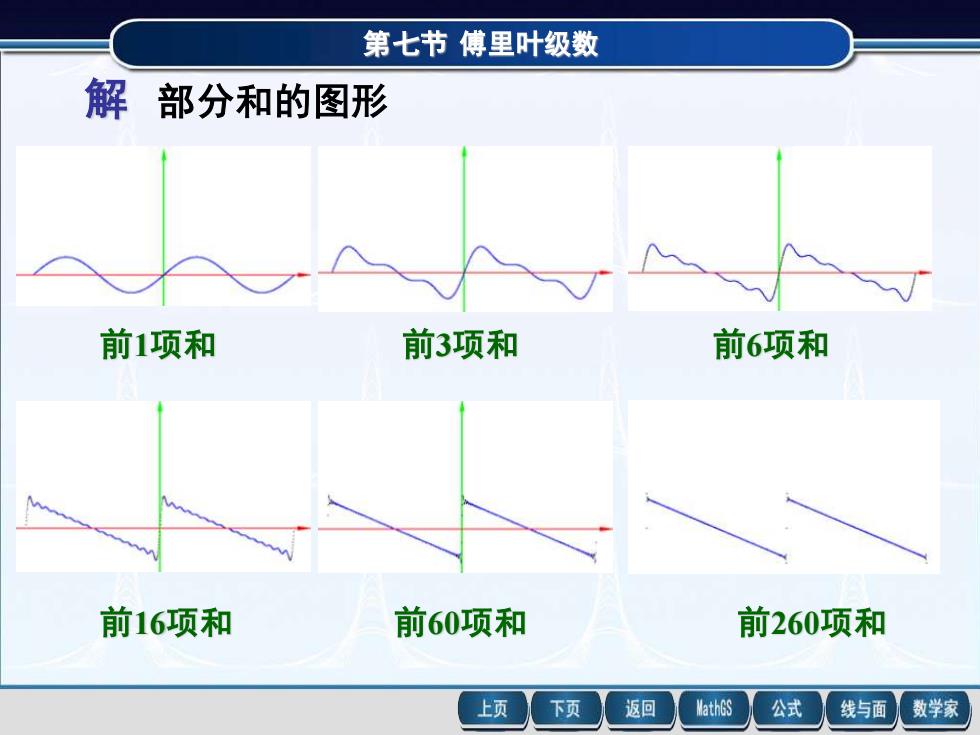
第七节 傅里叶级数 解 部分和的图形 前1项和 前3项和 前6项和 前16项和 前60项和 前260项和

第七节傅里叶级数由此可知(1)部分和Sk(x)是周期为2元的周期函数;(2)部分和 sk(x)在2k元(k=0,±1,±2,...)处不连续,在其他点处连续;(3)部分和数列 sk(x)收敛例1中的这些问题需要进行理论研究,这也是本节将要讨论的问题上页下页返回MathGS公式线与面数学家
第七节 傅里叶级数 由此可知 (1) 部分和 sk (x) 是周期为2 的周期函数; (2) 部分和 sk (x) 在2k (k=0,1, 2,.)处不连续,在 (3) 部分和数列 sk (x) 收敛. 其他点处连续; 例1中的这些问题需要进行理论研究,这也是本节 将要讨论的问题