
第八节一般周期函数的傅里叶级数周期为2的周期函数的傅里叶级数,傅里叶级数的复数形式返回MathGS公式上页下页线与面数学家
第八节 一般周期函数的傅里叶级数 *二、傅里叶级数的复数形式 一、周期为2l的周期函数的傅里叶级数

第八节一般周期函数的傅里叶级数一、周期为2的周期函数的傅里叶级数定理设周期为2l的周期函数f(x)满足收敛定理的条件,则它的傅里叶级数展开式为n元xn元xf(x)=号+2(b(xeEC),sin十COSan1n元xa,=L,ff(x)cosdx其中(n=0,1,2, ..)1n元xb,=,(x)sindx(n=1,2,3,..)1f(x)+f(xt)C=}xlf(x)=:2上页返回MathGS公式下页线与面数学家
第八节 一般周期函数的傅里叶级数 一、周期为2l的周期函数的傅里叶级数 定理 设周期为 2l 的周期函数 f (x) 满足收敛定理的 条件, 则它的傅里叶级数展开式为 ( ) , π sin π cos 2 ( ) 1 0 x C l n x b l n x a a f x n n n = + + = 其中 d ( 0,1,2, ), π ( ) cos 1 = = − x n l n x f x l a l l n d ( 1,2,3, ). π ( )sin 1 = = − x n l n x f x l b l l n , 2 ( ) ( ) | ( ) + = = − + f x f x C x f x

第八节一般周期函数的傅里叶级数8n元x当f(x)为奇函数时,f(x)=bn sin(xEC),1n=1n元xb,= (x)sindx其中(n = 1,2,3, .)18n元xaoZ当f()为偶函数时,f(x)=(xEC),十COSa121n=1n元xa, =(x)cosdx其中(n=0,1,2,..)1证明台返回MathGS公式上页下页线与面数学家
第八节 一般周期函数的傅里叶级数 当 f (x) 为奇函数时, ( ) , π ( ) sin 1 x C l n x f x b n = n = 其中 d ( 1,2,3, ). π ( )sin 2 0 = x n = l n x f x l b l n 当 f (x) 为偶函数时, ( ) , π cos 2 ( ) 1 0 x C l n x a a f x n = + n = 其中 d ( 0,1,2, ). π ( ) cos 2 0 = x n = l n x f x l a l n 第八节 一般周期函数的傅里叶级数 证明 作变量代换 , π l x z = 于是区间 –l x l 就变 换成 – z . 设函数 ( ) , π ( ) F z lz f x f = = 从而 F(z) 是周期为 2 的周期函数,并且它满足收敛定理的 条件, 将 F(z) 展开成傅里叶级数 ( cos sin ) , 2 ( ) 1 0 = = + + n an nz bn nz a F z 其中 ( ) cos d , π 1 π −π a = F z nz z n ( )sin d . π 1 π −π b = F z nz z n
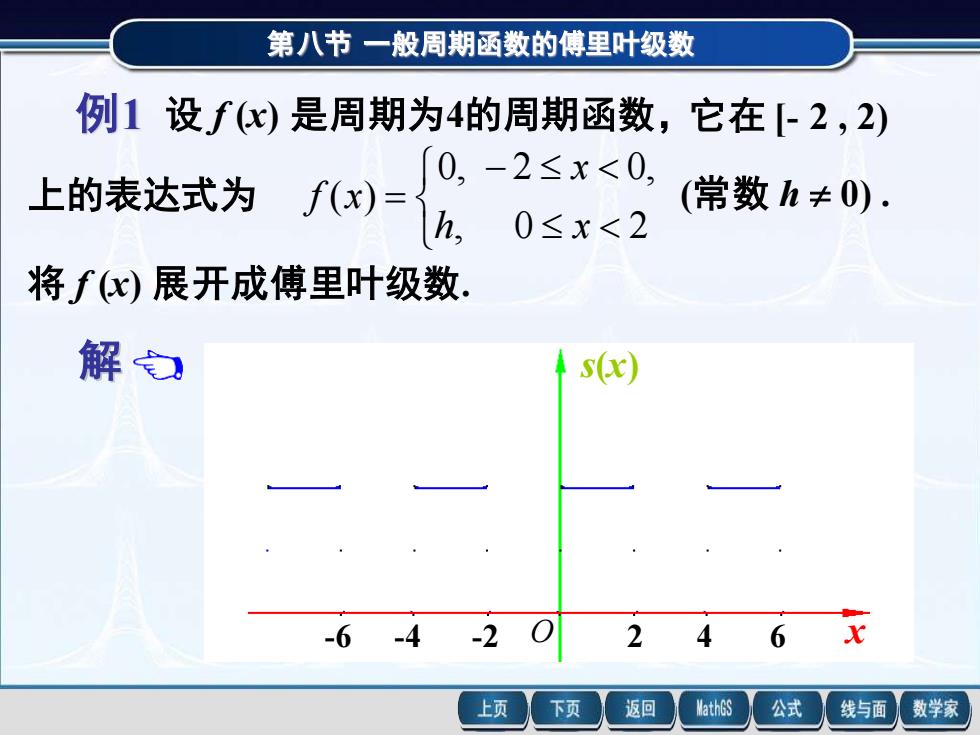
第八节一般周期函数的傅里叶级数例1设f(x)是周期为4的周期函数,它在[-2,2)0, -2≤x<0.(常数h±0)上的表达式为f(x)=h,0≤x<2将f(x)展开成傅里叶级数,解白s(x)x26-6-4-24下页返回MathGS公式数学家上页线与面
第八节 一般周期函数的傅里叶级数 例1 设 f (x) 是周期为4的周期函数, − = , 0 2 0, 2 0, ( ) h x x f x 第八节 一般周期函数的傅里叶级数 解 先求傅里叶系数,在这里 l = 2, = 2 0 d 2 π cos 2 1 x n x an h 例1 设 f (x) 是周期为4的周期函数, − = , 0 2 0, 2 0, ( ) h x x f x 它在 [- 2 , 2) 上的表达式为 将 f (x) 展开成傅里叶级数. (常数 h 0) . 0 ( 0); 2 π sin π 2 0 = = n n x n h = 2 0 0 ( )d 2 1 a f x x = + − 2 0 0 2 d 2 1 0d 2 1 x h x = h ; 它在 [- 2 , 2) 上的表达式为 将 f (x) 展开成傅里叶级数. (常数 h 0) . O x s(x) -6 -4 -2 2 4 6
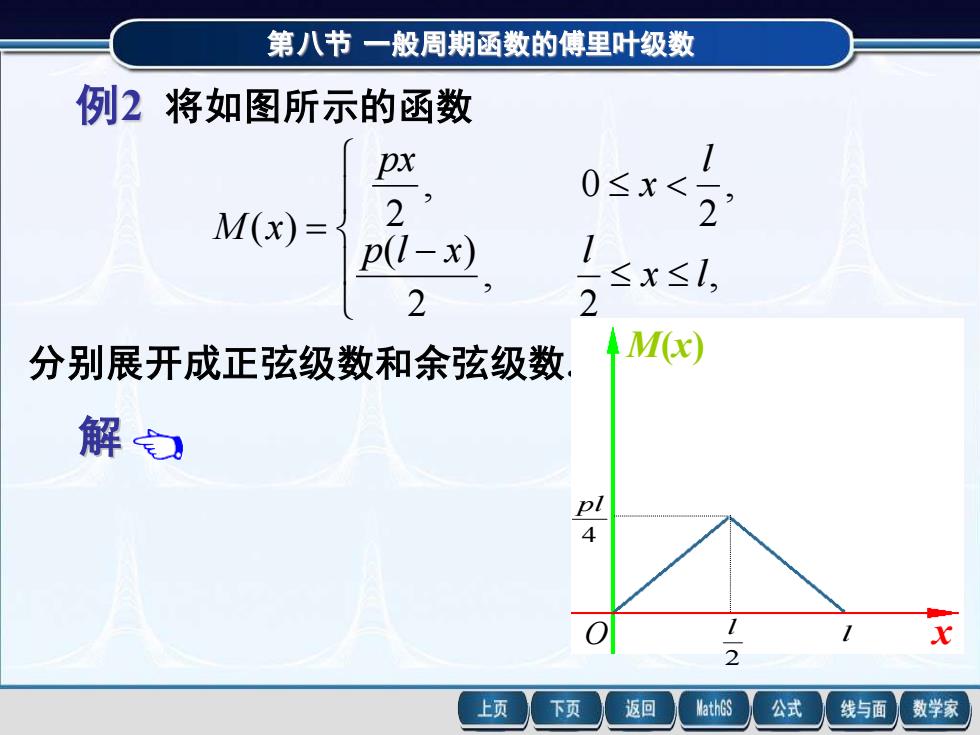
第八节一般周期函数的傅里叶级数例2将如图所示的函数1px0≤x<22M(x)三1p(l-x)≤x≤l,22 M(x)分别展开成正弦级数和余弦级数解台pl41-201x1返回MathGS公式上页下页线与面数学家
第八节 一般周期函数的傅里叶级数 例2 将如图所示的函数 − = , 2 , 2 ( ) , 2 , 0 2 ( ) x l p l x l l x px M x 第八节 一般周期函数的傅里叶级数 解 例2 将如图所示的函数 − = , 2 , 2 ( ) , 2 , 0 2 ( ) x l p l x l l x px M x 分别展开成正弦级数和余弦级数. 将 M(x) 进行奇延拓 O 2 l l 4 pl x M(x) 分别展开成正弦级数和余弦级数. O 2 l l 4 pl x M(x)