
第三节平面及其方程曲面方程与空间曲线方程的概念平面的点法式方程三、平面的一般方程四、两平面的夹角五、平面的参数方程返回MathGS公式上页下页线与面数学家
第三节 平面及其方程 二、平面的点法式方程 三、平面的一般方程 四、两平面的夹角 *五、平面的参数方程 一、曲面方程与空间曲线方程的概念

第三节 平面及其方程一曲面方程与空间曲线方程的概念1.曲面方程的定义定义如果曲面S与方程F(x,y,z)=0有下述关系:(1)曲面S上的任意点的坐标都满足此方程(2)不在曲面S上的点的坐标不满足此方程F(x, y, z) = 0则F(x,y,z)=0叫做曲面S的方程,曲面S叫做方程F(x,J,z)=0的图形XMathGS下页返回公式数学家上页线与面
第三节 平面及其方程 一、曲面方程与空间曲线方程的概念 S F(x, y, z) = 0 x y z 1. 曲面方程的定义 定义 如果曲面 S 与方程 F( x, y, z ) = 0 有下述 (1) 曲面 S 上的任意点的坐标都满足此方程, 则 F( x, y, z ) = 0 叫做曲面 S 的方程, 曲面 S 叫做方程 (2) 不在曲面 S 上的点的坐标不满足此方程, 关系: F( x, y, z ) = 0 的图形
第三节 平面及其方程如图所示的曲面叫莫比乌斯带返回MathGS公式上页下页线与面数学家
第三节 平面及其方程 如图所示的曲面叫 莫比乌斯带 x y z
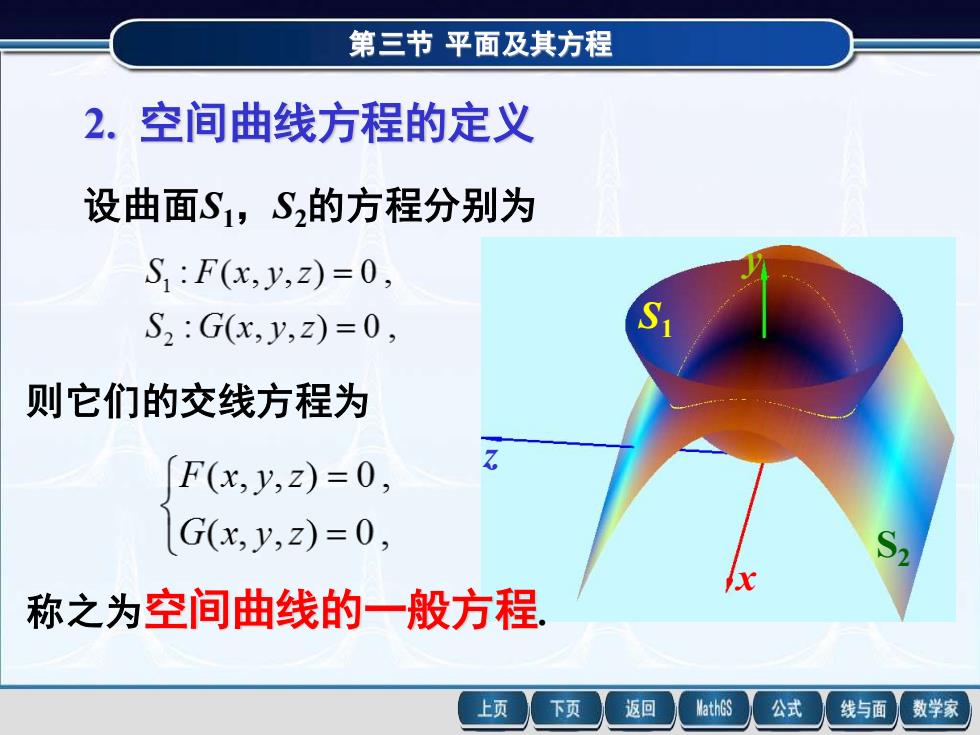
第三节 平面及其方程2.空间曲线方程的定义设曲面Su,S,的方程分别为S : F(x,y,z) = 0 ,SS2 : G(x,y,z) = 0 ,则它们的交线方程为7F(x,y,z)=0,G(x, y,z)= 0,S称之为空间曲线的一般方程MathGS公式下页返回线与面数学家上页
第三节 平面及其方程 2. 空间曲线方程的定义 设曲面S1,S2的方程分别为 x y z S1 S2 则它们的交线方程为 称之为空间曲线的一般方程

第三节 平面及其方程二、平面的点法式方程确定平面的方法:(1)一个点和一个非零向量;(2)三个不共线的点:(3)两条相交直线;(4)一个点和两个不共线的向量返回MathGS公式上页下页线与面数学家
第三节 平面及其方程 二、平面的点法式方程 (1) 一个点和一个非零向量; (2) 三个不共线的点; (3) 两条相交直线; 确定平面的方法: (4) 一个点和两个不共线的向量