
第一节向量及其线性运算、向量的概念一向量的线性运算空间直角坐标系三四、利用坐标作向量的线性运算五、向量的模、方向角、投影返回MathGS公式数学家上页下页线与面
第一节 向量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影

第一节向量及其线性运算向量的概念一、向量:既有大小,又有方向的量称为向量,又称矢量表示法:有向线段M,M,或a.向量的模:向量的大小,记作M,Ml或Iαl.自由向量:与起点无关的向量,M2+P2单位向量:模为1的向量,记作e。零向量:模为0的向量,记作0PM返回MathGS公式上页下页线与面数学家
第一节 向量及其线性运算 M2 M1 P2 P1 自由向量: 表示法: 向量的模: 向量的大小, 向量: 既有大小,又有方向的量称为向量,又称矢量 与起点无关的向量. 单位向量: 模为1的向量, 零向量: 模为0的向量, 有向线段 M1M2 记作 e . 或 a. 一、向量的概念 记作 |M1M2 | 或 | a | . 记作 0
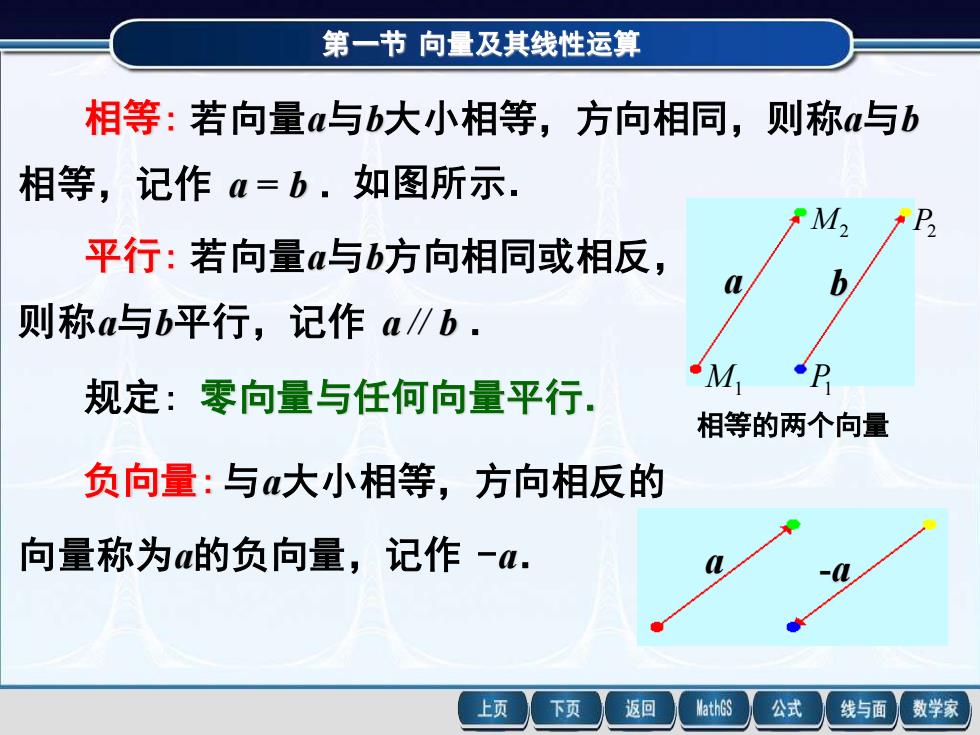
第一节向量及其线性运算相等:若向量a与b大小相等,方向相同,则称a与b相等,记作α=b.如图所示,MP2平行:若向量α与b方向相同或相反b1则称a与b平行,记作a/bPM规定:零向量与任何向量平行相等的两个向量负向量:与a大小相等,方向相反的向量称为α的负向量,记作一a.返回MathGS公式数学家上页下页线与面
第一节 向量及其线性运算 相等: 若向量a与b大小相等,方向相同,则称a与b 相等,记作 a = b . 平行: 若向量a与b方向相同或相反, 则称a与b平行,记作 a∥b . 如图所示. 负向量:与a大小相等,方向相反的 向量称为a的负向量,记作 -a. 规定: 零向量与任何向量平行. a -a M2 M1 P2 P1 相等的两个向量 a b

第一节向量及其线性运算共线:因平行向量可以平移到同一直线上,故两向量平行又称两向量共线:共面:若k(k≥3)个向量经平移可移到同一平面上则称这k个向量共面.z0Q0不共面共线共面返回MathGS公式上页下页线与面数学家
第一节 向量及其线性运算 x y z 共面 a b c O 共线: 因平行向量可以平移到同一直线上,故两向量 平行又称两向量共线 . 共面: 若k (k 3)个向量经平移可移到同一平面上, 则称这 k 个向量共面 . a b c x y 共线 O x y z 不共面 a b c O
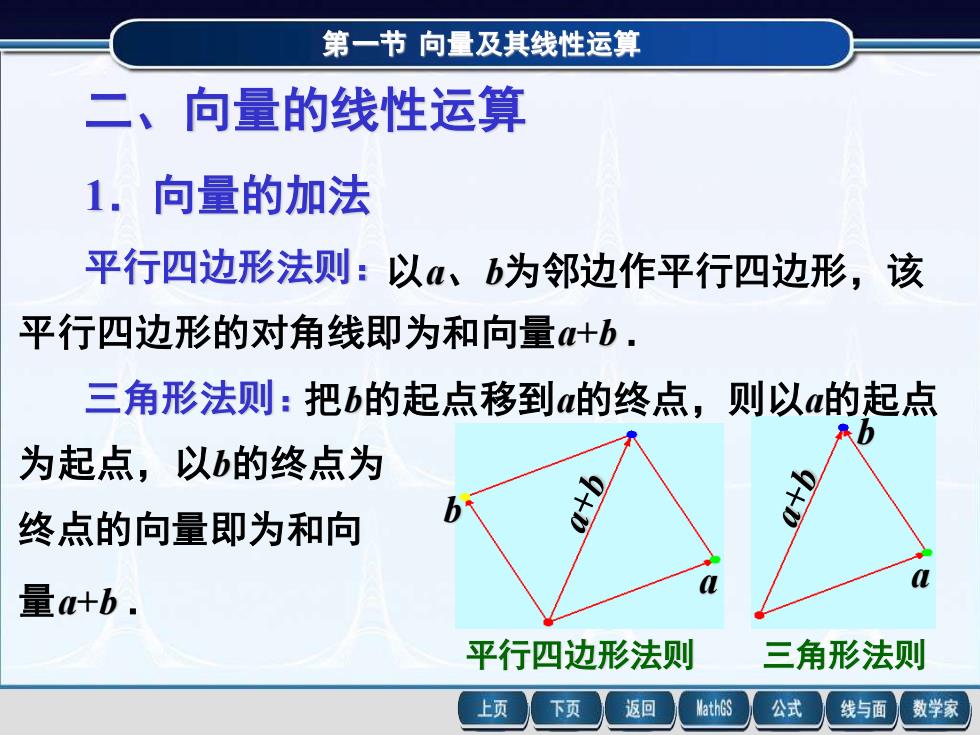
第一节向量及其线性运算二、向量的线性运算1.向量的加法平行四边形法则:以α、b为邻边作平行四边形,该平行四边形的对角线即为和向量a+b,三角形法则:把b的起点移到a的终点,则以a的起点h为起点,以b的终点为b终点的向量即为和向-a量a+b .三角形法则平行四边形法则MathGS数学家上页下页返回公式线与面
第一节 向量及其线性运算 平行四边形法则 三角形法则 a b a b 二、向量的线性运算 1.向量的加法 平行四边形法则:以a、b为邻边作平行四边形,该 平行四边形的对角线即为和向量a+b . 三角形法则:把b的起点移到a的终点,则以a的起点 为起点,以b的终点为 终点的向量即为和向 量a+b .