
第五节曲面及其方程曲面研究的基本问题旋转曲面三、柱面四、二次曲面五、高次代数曲面六、空间曲面欣赏返回MathGS公式上页下页线与面数学家
第五节 曲面及其方程 一、曲面研究的基本问题 二、旋转曲面 三、柱面 四、二次曲面 五、高次代数曲面 六、空间曲面欣赏

第五节曲面及其方程曲面研究的基本问题一、E在空间解析几何中,关于曲面的研究有下列两个基本问题:(1)已知一曲面作为点的几何轨迹时,求曲面方程2)已知方程时,研究它所表示的曲面的形状返回MathGS公式上页下页线与面数学家
第五节 曲面及其方程 一、曲面研究的基本问题 在空间解析几何中,关于曲面的研究有下列两个基 本问题: (1) 已知一曲面作为点的几何轨迹时,求曲面方程; (2) 已知方程时,研究它所表示的曲面的形状.

第五节曲面及其方程例1求动点到定点Mo(xo,yo,zo)距离为R的轨迹方程。解白例2 研究方程x2+y2+z2-2x+4y=0 表示怎样的曲面。解白如下形式的三元二次方程(A+0)A(x? + y? + z2)+ Dx+ Ey + Fz+G = 0都可通过配方研究它的图形上页下页返回MathGS公式数学家线与面
第五节 曲面及其方程 第五节 曲面及其方程 故所求方程为 M (x, y,z), 特别,当M0在原点时,球面方程为 解 设轨迹上动点为 , M0 M = R 即 依题意 ( ) ( ) ( ) . 2 0 2 0 2 x − x0 + y − y + z − z = R ( ) ( ) ( ) . 2 2 0 2 0 2 x − x0 + y − y + z − z = R . 2 2 2 2 x + y + z = R 例1 求动点到定点 ( , , ) 0 0 0 0 M x y z 方程. 距离为 R 的轨迹 M0 M x z O 例1 求动点到定点 方程. 距离为 R 的轨迹 例2 研究方程 的曲面. 表示怎样 第五节 曲面及其方程 解 例2 研究方程 2 4 0 2 2 2 x + y + z − x + y = 的曲面. 表示怎样 球心为 配方得 5 . (1, 2, 0), M0 − 可见此方程表示一个球面, 半径为 ( 1) ( 2) 5 . 2 2 2 x − + y + + z = x y z 如下形式的三元二次方程 ( A≠ 0 ) 都可通过配方研究它的图形

第五节曲面及其方程二、旋转曲面引例在MathGS中观察xOv面上的抛物线y=x?分别绕三条坐标和任意过原点的直线旋转而成的曲面xX7x7绕轴绕x轴绕y轴绕向量(1,1,1)动画包MathGS上页下页返回公式线与面数学家
第五节 曲面及其方程 二、旋转曲面 在MathGS中观察xOy面上的抛物线y=x 引例 2 分别 绕三条坐标和任意过原点的直线旋转而成的曲面. 绕x轴 x y z 绕y轴 x y z 绕z轴 x y z 绕向量(1,1,1) x y z 第五节 曲面及其方程 动画 绕x轴 绕z轴 绕y轴 绕向量
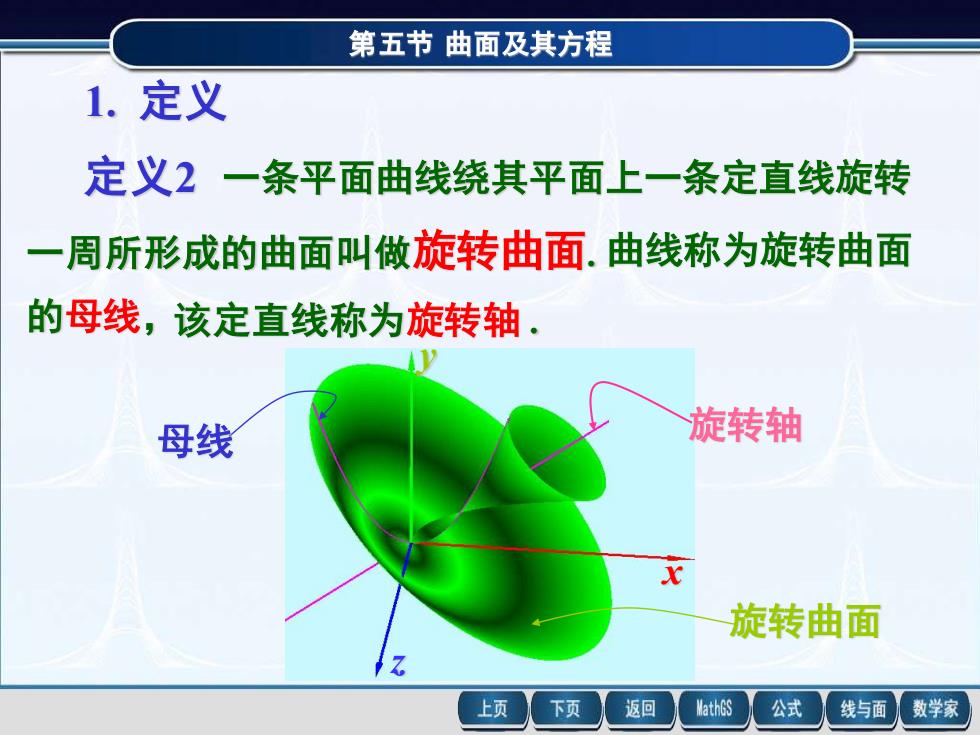
第五节曲面及其方程1.定义定义2一条平面曲线绕其平面上一条定直线旋转旋转曲面曲线称为旋转曲面一周所形成的曲面叫做门的母线,该定直线称为旋转轴旋转轴母线x旋转曲面返回MathGS下页公式线与面数学家上页
第五节 曲面及其方程 x y z 1. 定义 定义2 一条平面曲线绕其平面上一条定直线旋转 一周所形成的曲面叫做旋转曲面. 曲线称为旋转曲面 的母线, 母线 旋转轴 旋转曲面 该定直线称为旋转轴