
第八节多元函数的极值及其求法一、多元函数的极值最值及其应用三、条件极值返回MathGS公式上页下页线与面数学家
第八节 多元函数的极值及其求法 一、多元函数的极值 二、最值及其应用 三、条件极值

第八节多元函数的极值及其求法一、兰多元函数极值1.二元函数极值的定义定义设 z=f(x,J)的定义域为D,Po(xo,yo)为D的内点。若存在P的某个邻域U(Po)CD,使得对于该邻域内异于Po的任何点(x,J),都有f (x,y) <f(xo,yo),则称函数z=f(x,y)在点(xoyo)有极大值f(xoyo),点(xo,Jo)称为函数f(x,)的极大值点MathGS上页下页返回公式线与面数学家
第八节 多元函数的极值及其求法 一、多元函数极值 1. 二元函数极值的定义 定义设 z = f (x , y)的定义域为D,P0 (x0 , y0 )为D的内 点. 若存在P0的某个邻域U(P0 ) D,使得对于该邻域 内异于P0的任何点(x , y),都有 f (x , y) < f (x0 , y0 ), 则称函数 z = f (x , y) 在点 (x0 , y0 ) 有极大值 f (x0 , y0 ), 点(x0 , y0 )称为函数f(x , y) 的极大值点;

第八节多元函数的极值及其求法都有若对于该邻域内异于P的任何点(αx,y),f (x,y) >f(xo,yo),则称函数z=f(x,y)在点(xo,yo)有极小值f(xo,yo),点(xo,y)称为函数f(x,y)的极小值点极大值与极小值统称为极值,使函数取得极值的点称为极值点返回MathGS公式上页下页线与面数学家
第八节 多元函数的极值及其求法 若对于该邻域内异于P0的任何点(x , y),都有 f (x , y) > f (x0 , y0 ), 则称函数 z = f (x , y) 在点 (x0 , y0 ) 有极小值 f (x0 , y0 ), 点(x0 , y0 )称为函数f(x , y) 的极小值点. 极大值与极小值统称为极值,使函数取得极值的 点称为极值点.
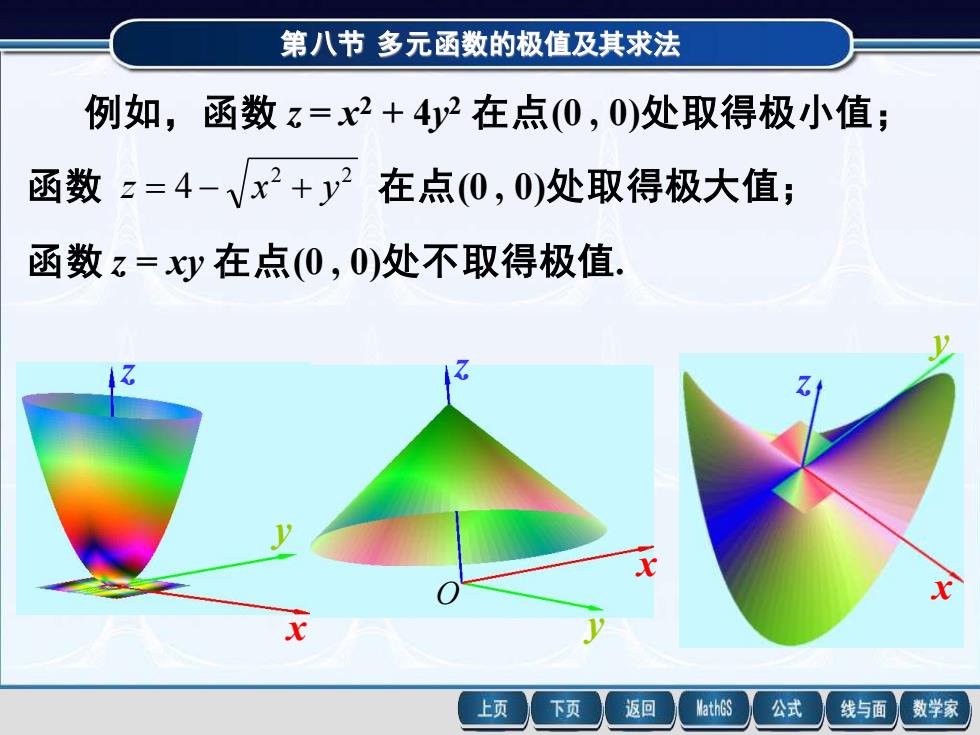
第八节多元函数的极值及其求法例如,函数z=x2+4v2在点(0,0)处取得极小值函数 z=4-x2+y2 在点(0,0)处取得极大值;函数z=xy在点(0,0)处不取得极值71x1XMathGS下页返回公式数学家上页线与面
第八节 多元函数的极值及其求法 例如,函数 z = x 2 + 4y 2 在点(0 , 0)处取得极小值; 函数 2 2 z = 4 − x + y 在点(0 , 0)处取得极大值; 函数 z = xy 在点(0 , 0)处不取得极值. z x y z x y z x y O
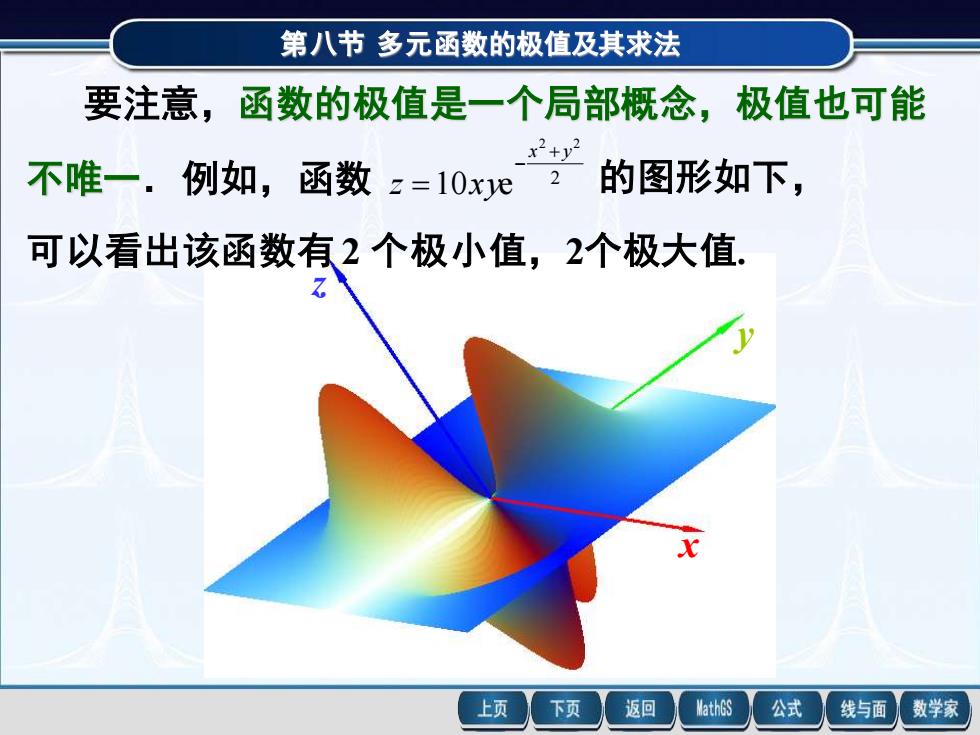
第八节多元函数的极值及其求法要注意,函数的极值是一个局部概念,极值也可能22+y的图形如下,不唯一.例如,函数 z=10xje2可以看出该函数有2个极小值,2个极大值7MathGS上页下页返回公式线与面数学家
第八节 多元函数的极值及其求法 x y z 要注意,函数的极值是一个局部概念,极值也可能 不唯一.例如,函数 2 2 2 10 e x y z x y + − = 的图形如下, 可以看出该函数有 2 个极小值,2个极大值