
定义1.设非空点集DcR2,映射f:D→R称为定义 在D上的二元函数,记作 z=f(x,y)或a=f(P),P∈D 点集D称为函数的定义域;数集{zz=f(P),P∈D} 称为函数的值域. 特别地,当n=3时,有三元函数 u=f(x,y,z),(x,y,2)EDCR3 般n元函数可表示为 u=f(x1,x2,.,xn)或u=f(P),P∈D
定义1. 设非空点集 点集 D 称为函数的定义域 ; 数集 z z f P ,P D ( ) 称为函数的值域 . 特别地 , 当 n = 3 时, 有三元函数 映射 称为定义 在 D 上的二元函数 , 记作 一般n元函数可表示为
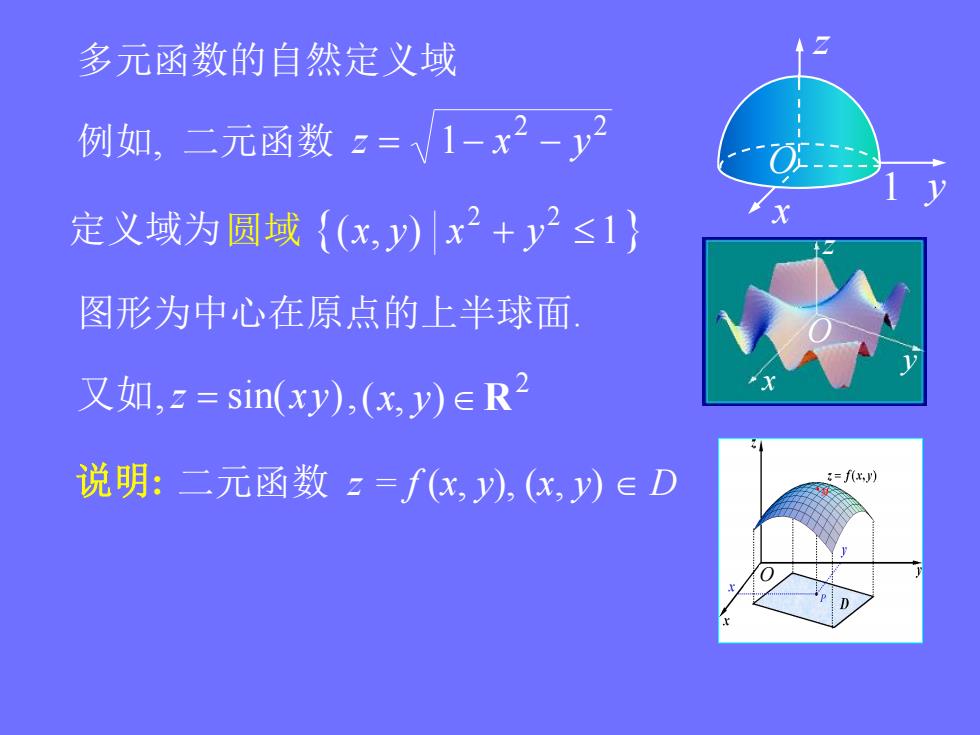
多元函数的自然定义域 例如,二元函数=√1-x2-y 定义域为圆域{(x,y)x2+y2≤1} 图形为中心在原点的上半球面 又如,z=sin(xy),(x,y)∈R2 说明:二元函数z=f(x,y),(x,y)∈D =f(,)
x z y 例如, 二元函数 2 2 z 1 x y 定义域为 ( , ) 1 2 2 圆域 x y x y 说明: 二元函数 z = f (x, y), (x, y) D 图形为中心在原点的上半球面. 又如,z sin(xy), 1 2 (x, y)R x y z O O O 多元函数的自然定义域