
第五节 第八章 曲面及其方程 一、曲面研究的基本问题 二、旋转曲面 三、柱面 四、二次曲面
四、二次曲面 第五节 一、曲面研究的基本问题 二、旋转曲面 三、柱面 曲面及其方程 第八章

一、曲面研究的基本问题 关于曲面研究有下列两个基本问题: (1)已知一曲面作为点的几何轨迹时,建立曲面的方程 (2)已知坐标x、y和间方程时,研究方程所表示的曲面 形状
一、曲面研究的基本问题 关于曲面研究有下列两个基本问题: (2) 已知坐标x、y和z间方程时,研究方程所表示的曲面 (1) 已知一曲面作为点的几何轨迹时,建立曲面的方程; 形状

例1,求动点到定点Mo(xo,0,2o)距离为R的轨迹 方程 解:设轨迹上动点为M(x,y,z),依题意M,M=R 即 V(x-x)2+(y-y0)2+(2-0)2=R 故所求方程为 (x-x0)2+(y-%)2+(:-0)2=R2 特别,当M在原点时,球面方程为 x2+y2+2=R2 z=±√R2-x2-y2表示上(下)球面
故所求方程为 例1. 求动点到定点 方程. 特别,当M0在原点时,球面方程为 解: 设轨迹上动点为 即 依题意 距离为 R 的轨迹 M O x y z M0 表示上(下)球面 . x x y y z z R 2 0 2 0 2 0 ( ) ( ) ( ) 2 2 0 2 0 2 0 (x x ) ( y y ) (z z ) R 2 2 2 2 x y z R

例2.研究方程x2+y2+z2-2x+4y=0表示怎样 的曲面, 解:配方得 (x-1)2+y+2)2+z2=5 可见此方程表示一个球面 球心为Mo(1,-2,0),半径为√5 说明:如下形式的三元二次方程(A≠0) A(x2+y2+z2)+Dx+Ey+Fz+G=0 都可通过配方研究它的图形.其图形可能是 个球面,或点,或虚轨迹
例2. 研究方程 解: 配方得 M 0 (1, 2, 0), 5 可见此方程表示一个球面 说明:如下形式的三元二次方程 ( A≠ 0 ) 都可通过配方研究它的图形.其图形可能是 的曲面. 表示怎样 球心为 半径为 一个球面 , 或点 , 或虚轨迹
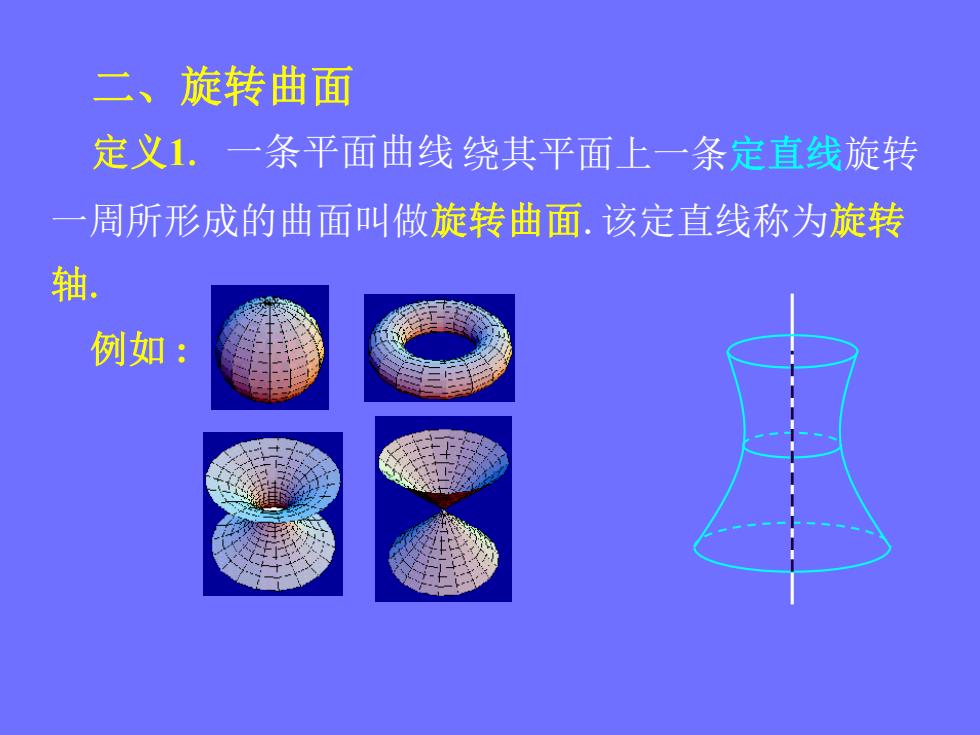
二、旋转曲面 定义1,一条平面曲线绕其平面上一条定直线旋转 一周所形成的曲面叫做旋转曲面.该定直线称为旋转 轴. 例如:
定义1. 一条平面曲线 二、旋转曲面 绕其平面上一条定直线旋转 一周所形成的曲面叫做旋转曲面.该定直线称为旋转 轴. 例如 :