一、 利用直角坐标系计算二重积分 如果积分区域为:a≤x≤b, p(x)≤y≤p2(x) [X-型] y=Q(x) =p2(x) D D y=9(x) 其中函数p(x)、p2(x)在区间[a,b]上连续, 则 nfd=dy网fx
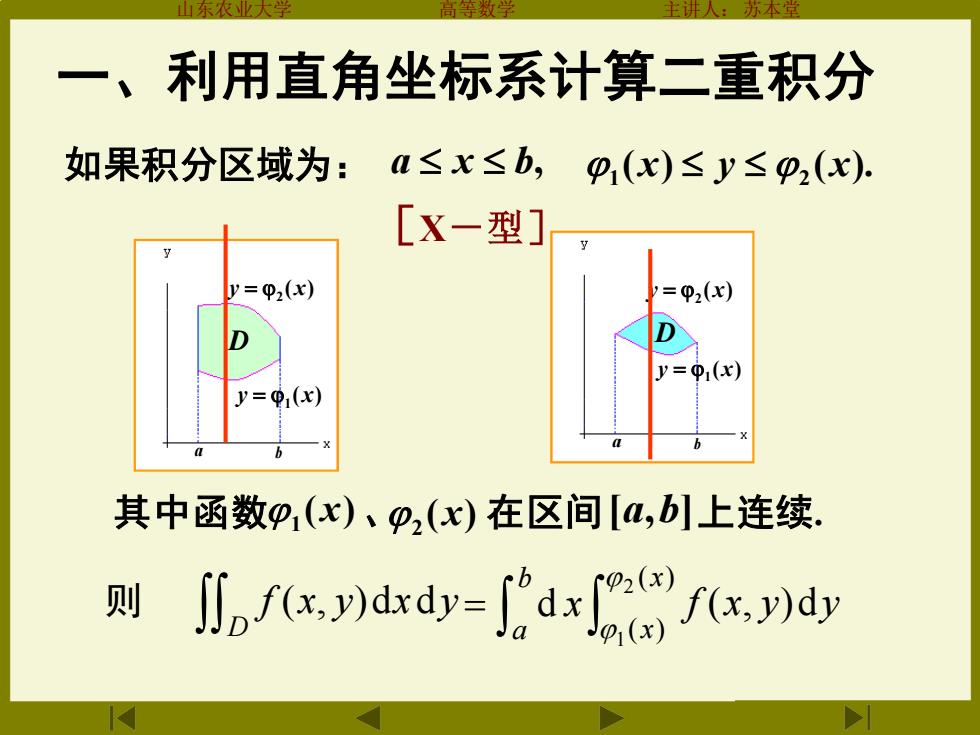
山东农业大学 高等数学 主讲人:苏本堂 如果积分区域为: a x b, ( ) ( ). 1 x y 2 x [X-型] ( ) 2 y = x a b D ( ) 1 y = x D a b ( ) 2 y = x ( ) 1 y = x 其中函数 ( ) 、 在区间 上连续. 1 x ( ) 2 x [a,b] 一、利用直角坐标系计算二重积分 D f (x, y)dxdy f x y y x x ( , )d ( ) ( ) 2 1 = b a 则 d x

山东农业大 等数 主讲 苏本堂 如果积分区域为:c≤y≤d, p(y)≤x≤p2(Jy) [Y-型] x=0() x=o(y) x三p2(Jy) a=广f D X型区域的特点:穿过区域且平行于y轴的直 线与区域边界相交不多于两个交点。 Y型区域的特点:穿过区域且平行于x轴的直 线与区域边界相交不多于两个交点
山东农业大学 高等数学 主讲人:苏本堂 如果积分区域为: c y d, ( ) ( ). 1 2 y x y [Y-型] ( ) 2 x = y ( ) 1 x = y D c d c d ( ) 2 x = y ( ) 1 x = y D ( , ) ( , ) . ( ) ( ) 2 1 = D d c y y f x y d dy f x y dx X型区域的特点: 穿过区域且平行于y轴的直 线与区域边界相交不多于两个交点. Y型区域的特点:穿过区域且平行于x轴的直 线与区域边界相交不多于两个交点

注:(I)若积分区域既是X-型区域又是Y-型区域, 则有 ∬nfx,y)drdy ↑y (x) -af x=必y) =2(y) D =dyfct y=0(x) a X bx 为计算方便,可选择积分序,必要时还可以交换积分序 (2)若积分域较复杂,可将它分成若干y X型域或Y型域,则 川n=∬o+小n+川 3
山东农业大学 高等数学 主讲人:苏本堂 o x y 注: (1) 若积分区域既是X–型区域又是Y –型区域 , D f (x, y)dxdy 为计算方便,可选择积分序, 必要时还可以交换积分序. ( ) 2 y = x o x y D a b ( ) 1 x = y ( ) 2 x = y d c 则有 x ( ) 1 y = x y f x y y x x ( , )d ( ) ( ) 2 1 = b a d x f x y x y y ( , )d ( ) ( ) 2 1 = d c d y (2) 若积分域较复杂,可将它分成若干 D1 D2 D3 X-型域或Y-型域 , = + + D D1 D2 D3 则

苏本 (3)二重积分化累次积分的步骤 ①画域,②选序,③定限 (4)累次积分中积分的上限不小于下限 (5)二重积分化累次积分定限是关键,积分限 要根据积分区域的形状来确定,这首先要画好 区域的草图,特别要画好围成D的几条边界线
山东农业大学 高等数学 主讲人:苏本堂 (3)二重积分化累次积分的步骤 ①画域,②选序,③定限 (4)累次积分中积分的上限不小于下限 (5)二重积分化累次积分定限是关键,积分限 要根据积分区域的形状来确定,这首先要画好 区域的草图,特别要画好围成D的几条边界线
若是X一型,就先y后x, 若是Y一型,就先x后y, 注意内层积分限是外层积分变量的函数,外层 积分限是常数。 例1 改变积分fx,y)的次序. 解 积分区域如图,既是X一型, 也是Y一型 0.e y=1-x 0.6 原式=fx,. 0.2 0.20.40.60.81
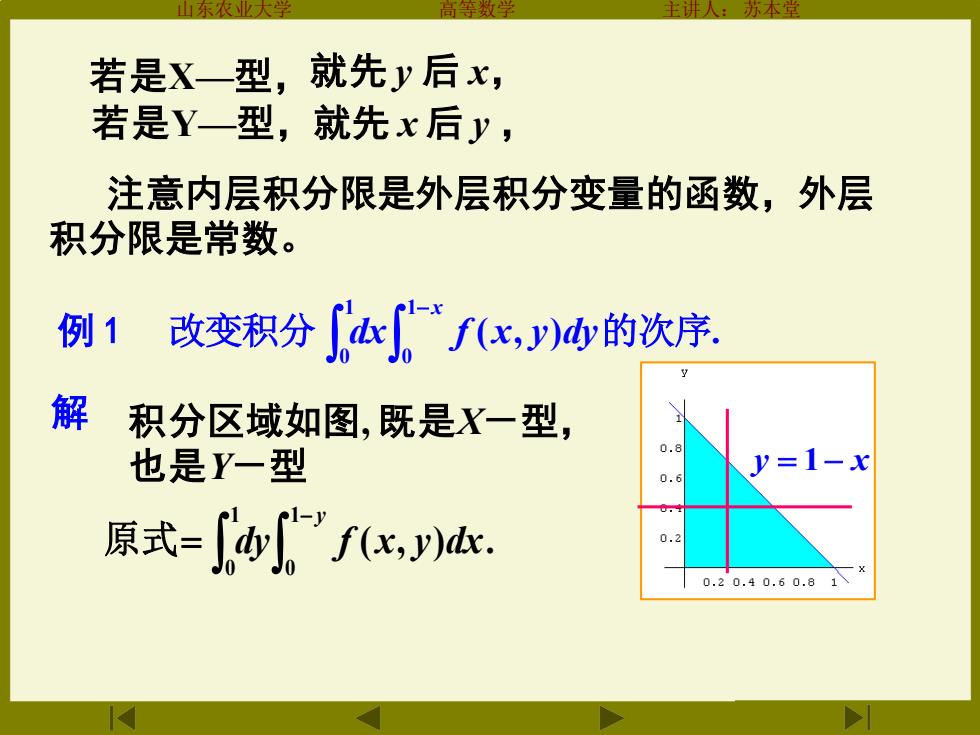
山东农业大学 高等数学 主讲人:苏本堂 若是X—型,就先 y 后 x, 若是Y—型,就先 x 后 y , 注意内层积分限是外层积分变量的函数,外层 积分限是常数。 例 1 改变积分 − x dx f x y dy 1 0 1 0 ( , ) 的次序. 解 积分区域如图, 既是X-型, 也是Y-型 y = 1− x 原式 − = y dy f x y dx 1 0 1 0 ( , )