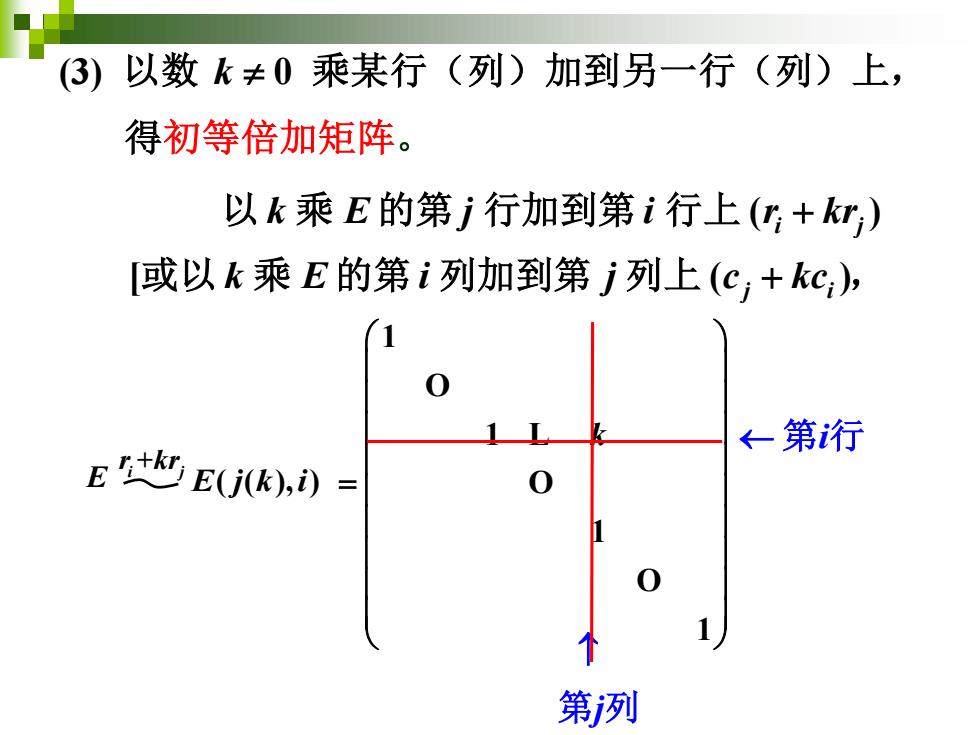
3) 以数k≠0乘某行(列)加到另一行(列)上, 得初等倍加矩阵。 以k乘E的第j行加到第i行上(+kr) [或以k乘E的第i列加到第j列上(c,+kc), ←第行 EE(j(k),i)= 第冽
或以 乘 的第 列加到第 列上 , 以 乘 的第 行加到第 行上 [ ( ) ( ) j i i j k E i j c kc k E j i r kr + + 1 1 1 1 k = O L O O 第i行 j 第 列 (3) 以数 k 0 乘某行(列)加到另一行(列)上, 得初等倍加矩阵。 r kr i j + E E j k i ( ( ), )

三种初等矩阵的性质: 初等矩阵是可逆的,逆矩阵仍为初等矩阵。 E(i,j川-E到=-1≠0,且Ei,)'=E(i,)月 E(k)训=kE=k≠0,且E(ik)=E(片 E(jk),)|E到=1≠0,且E(jk),)1=E(j(-),). 所以: 初等矩阵不但可逆,而且其逆矩阵仍为同类项的 初等矩阵
1 E i j E i j ( , ) ( , ); − 且 = 初等矩阵是可逆的,逆矩阵仍为初等矩阵。 三种初等矩阵的性质: E i j ( , ) 1 3 r r = − E = − 1 0, 1 1 E i k E i ( ( )) ( ( )); k − E i k k E k ( ( )) = = 0, 且 = 1 E j k i E j k i ( ( ), ) ( ( ), ). − E j k i ( ( ), ) 且 = − i j r kr − = E = 1 0, 所以: 初等矩阵不但可逆,而且其逆矩阵仍为同类项的 初等矩阵

初等矩阵的应用 对A进行初等行变换就相当于以相应的初等矩阵左乘矩阵A: L 12 L 11 012 1n M M M M M M L L ai ai A= M M M M M M =E(i,j)4 an 0j2 L L M M M am2 L . a mn 1 列 O M E(i,j)A= i2 in 列
11 12 1 1 2 1 2 1 2 n i i in j j jn m m mn a a a a a a A a a a a a a = L M M M L M M M L M M M L 11 12 1 1 2 1 2 1 2 n j j jn i i in m m mn a a a a a a a a a a a a L M M M L M M M L M M M L r r i j = E i j A ( , ) ; E i j A ( , ) = 11 12 1 1 2 1 2 1 2 1 0 1 1 0 1 n i i in j j jn m m mn a a a a a a a a a a a a L O M M M L O M M M L O M M M L j列 i列 对A进行初等行变换就相当于以相应的初等矩阵左乘矩阵A: 初等矩阵的应用