《线性代数》课程教学课件（PPT讲稿，B）第二章 矩阵与向量_2-4 矩阵的秩

问题：矩阵的行秩乡 矩阵的列秩 定理 矩阵的初等行（列）变换不改变矩阵的行（列）秩。 2.4.1: a 证：把A,mn按行分块，设Axn= &2 M (1)对换矩阵A的两行 A的行向量组所含向量未变，所以向量组的秩不变， 所以矩阵A的行秩不变。 即：交换两行不改变矩阵的行秩。 (2)用非零常数乘以A的第行

问题：矩阵的行秩 ? ＝ 矩阵的列秩 矩阵的初等行(列)变换不改变矩阵的行(列)秩。 证：把 A m n 按行分块，设 1 2 m n m A      =            M （1）对换矩阵A的两行 A的行向量组所含向量未变，所以向量组的秩不变， 所以矩阵A的行秩不变。 （2）用非零常数k乘以A的第i行 定理 2.4.1： 即:交换两行不改变矩阵的行秩

1 a M M 显然，向量组c1,L,kQ,L,am A= 01 kai =A, 可以由向量组a1L,c,L,Cm M M 线性表示； m 而向量组必1，L,C,L,0m也可以由向量组01，L,kC,L,Cm 线性表示。 所以矩阵A的行向量组与A,的行向量组等价， 又等价的向量组有相同的秩， .A的行秩=A,的行秩， 即A的某一行乘以非零的数k不改变矩阵的行秩

1 1 2 i kr i i m m A A k                   = =                     M M M M : 显然，向量组 1 , , , , i m    L L k 可以由向量组 1 , , , ,    L Li m 线性表示； 而向量组 1 , , , ,    L Li m 也可以由向量组 1 , , , , i m    L L k 线性表示。 所以矩阵 A 的行向量组与 A2 的行向量组等价， 又等价的向量组有相同的秩，  A 的行秩＝ A2 的行秩， 即A的某一行乘以非零的数k不改变矩阵的行秩

(3)非零常数k乘以第行后加到第行上 a M M 显然，A中的行向量组 C 可以由A的行向量组线性表示 A= M 。 M =A而A的行向量组可以由 aj +ka; A中的行向量组线性表示。 M M Cm m 所以两个向量组等价，所以行向量组的秩不变， 所以矩阵的行秩不变。 即A的某一行乘以数k加到另一行上不改变矩阵的行秩

（3）非零常数k乘以第i行后加到第j行上 1 1 3 j i i i r kr j j i m m A A k          +                     = =         +                 M M M M M M : 显然， A3 中的行向量组 可以由 A 的行向量组线性表示 而 A 的行向量组可以由 A3 中的行向量组线性表示。 所以两个向量组等价，所以行向量组的秩不变， 所以矩阵的行秩不变。 即A的某一行乘以数k加到另一行上不改变矩阵的行秩

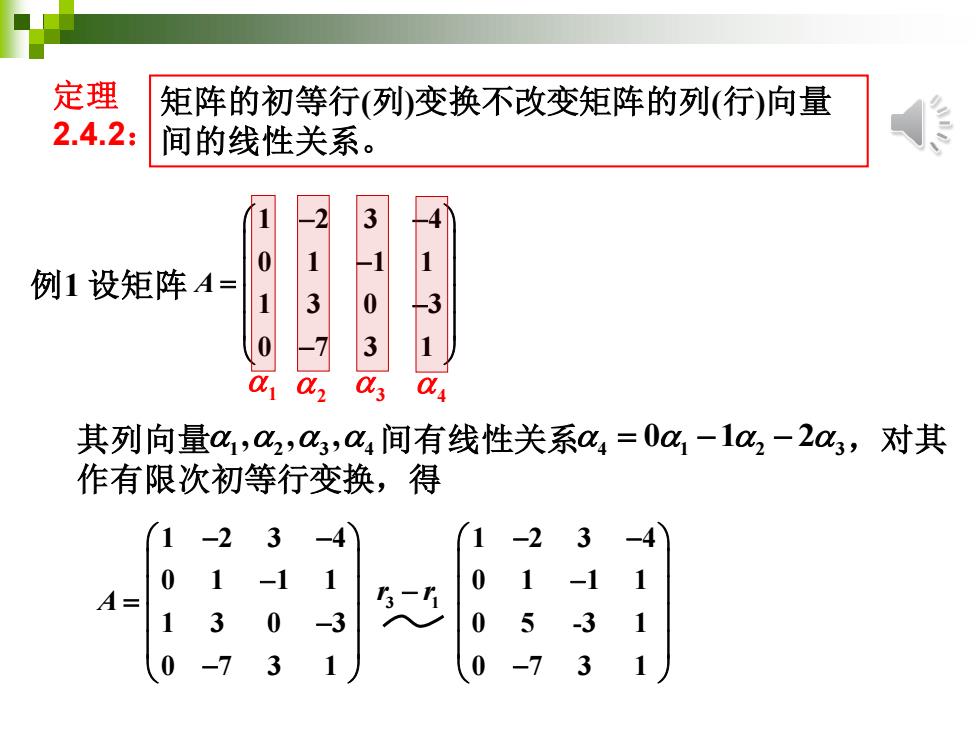
定理 矩阵的初等行（列变换不改变矩阵的列（行）向量 2.4.2: 间的线性关系。 -2 3 0 1 例1设矩阵A= 1 3 0 -3 7 3 a, 3 其列向量a,a2,a3,a4间有线性关系a4=0a%1-1ax2-2c,对其 作有限次初等行变换，得 1 -2 3 -4 1-2 3 0 1 -1 1 0 1 A- 1 3 0 -3 0 5 -3 -7 3 1 0 -7 3

1 2 3 4 0 1 1 1 1 3 0 3 0 7 3 1 A   − −   −   =   −     − 矩阵的初等行(列)变换不改变矩阵的列(行)向量 间的线性关系。 定理 2.4.2： 例1 设矩阵 其列向量 间有线性关系 ，对其 作有限次初等行变换，得 1 2 3 4     , 4 1 2 3     = − − 0 1 2 1 2 3 4 0 1 1 1 1 3 0 3 0 7 3 1 A   − −   −   =   −     − 3 1 r r − 1 2 3 4 0 1 1 1 0 5 -3 1 0 7 3 1   − −   −         − 1  2  3 4

1-2 3 -4 1 -2 3 -4 3-5 0 1 -1 1 4+25 0 1 -1 1 0 0 2 -4 1 0 +72 0 1 -2 0 0 -4 8 0 0 0 0 1-20 2 1000Y +3 0 1 0 1 1+2 010-1 0 01 -2 001 -2 =(B,B2,B,B4)=B 1-3 0 00 0 000 0) 行最简形 B B2 B:B 矩阵B作为矩阵A的行最简形，其B列向量之间的线性关系为 B,=0B-B2-2p3, 由此可见，矩阵A和矩阵B列向量有相同的线性关系。 即：矩阵的初等行变换不改变矩阵的列向量间的线性关系。 所以矩阵的初等行变换不改变矩阵的列秩

4 2 r r + 7 3 2 r r − 5 1 2 3 4 0 1 1 1 0 0 2 -4 0 0 -4 8   − −   −         1 2 2 r 4 3 r r + 2 1 2 3 4 0 1 1 1 0 0 1 -2 0 0 0 0   − −   −         1 3 r r −3 2 3 r r + 1 -2 0 2 0 1 0 -1 0 0 1 -2 0000             1 2 r r + 2 1 0 0 0 0 1 0 -1 0 0 1 -2 0 0 0 0             = , , , (    1 2 3 4 ) = B 矩阵B作为矩阵A的行最简形，其B列向量之间的线性关系为     4 1 2 3 =0 2 , − − 由此可见，矩阵A和矩阵B列向量有相同的线性关系。 行最简形  1  2  3  4 即：矩阵的初等行变换不改变矩阵的列向量间的线性关系。 所以矩阵的初等行变换不改变矩阵的列秩