
2.三阶行列式 1X1+12X2+41gK3=b, 讨论三元线性方程组 021七,+022X2+02aX3=b2 (1.2) L31X1+032火2+03X3=bg 定义对于有9个元素4:排成3行3列的式子 11012 13 L21 L22 L23 (1.3) 记 L31 l32 33 主对角线 2 ,013 021 3 =011L22L3+012023L31+01321L32 副对角线 32 33 -L13L22L31-012021033-11023L32 称为三阶行列式
2.三阶行列式 记 称为三阶行列式. 11 12 13 21 22 23 31 32 33 a a a a a a a a a = 11 22 33 12 23 31 13 21 32 13 22 31 12 21 33 11 23 32 a a a a a a a a a a a a a a a a a a + + − − − 主对角线 副对角线 定义 对于有9个元素 aij 排成3行3列的式子 讨论三元线性方程组 + + = + + = + + = 31 1 32 2 33 3 3 21 1 22 2 23 3 2 11 1 12 2 13 3 1 a x a x a x b a x a x a x b a x a x a x b (1.2) 11 12 13 21 22 23 31 32 33 a a a a a a a a a (1.3)
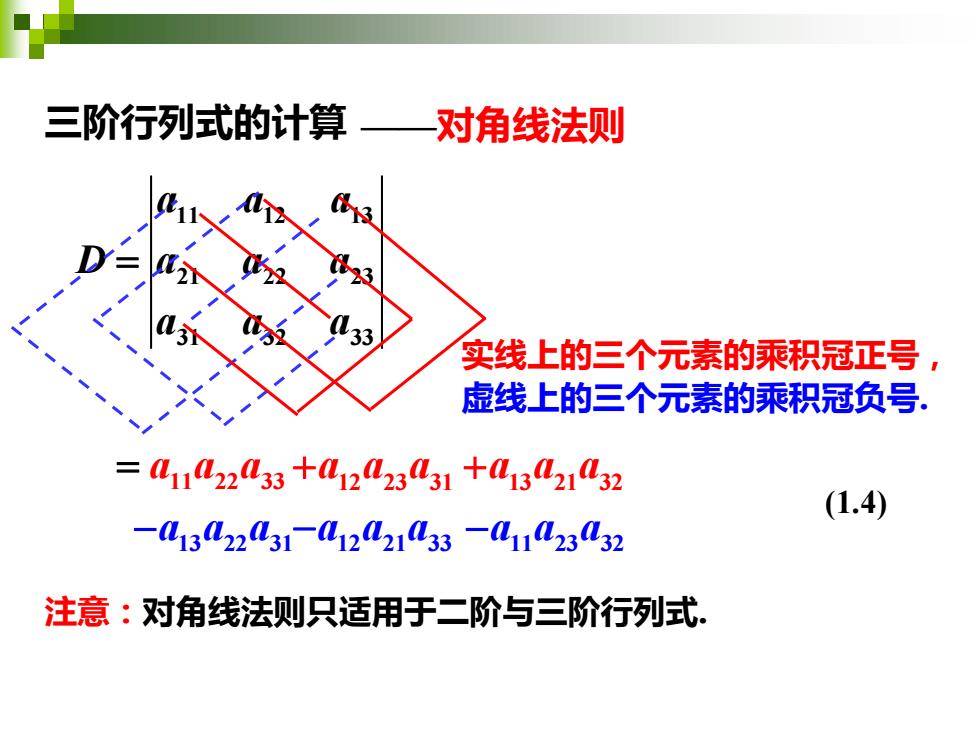
三阶行列式的计算一对角线法则 33 实线上的三个元素的乘积冠正号, 虚线上的三个元素的乘积冠负号。 =41422433+a12423431+01342142 (1.4) -13L2231-12L21L33-L11L23L32 注意:对角线法则只适用于二阶与三阶行列式
三阶行列式的计算 ——对角线法则 11 12 13 21 22 23 31 32 33 a a a D a a a a a a = 13 21 32 = a a a 11 22 33 +a a a 12 23 31 +a a a 13 22 31 −a a a 12 21 33 −a a a 11 23 32 −a a a 注意:对角线法则只适用于二阶与三阶行列式. 实线上的三个元素的乘积冠正号, 虚线上的三个元素的乘积冠负号. (1.4)

例1计算行列式 解 按对角线法则,有 D=3×(-3)×2+2×(-5)×3+2×4×4 -3×(-3)×4-2×2×2-3×4×(-5) =-18-30+32+36+60-8 =72
323 2 -3 4 4 -5 2 例1 计算行列式 D = 解 按对角线法则,有 D = 3 ( 3) 2 − − − 3 ( 3) 4 = − − + + + − 18 30 32 36 60 8 = 72 + − 2 ( 5) 3+ 244 − 222 − − 3 4 ( 5)

对于三元线性方程组(1.2),若其系数行列式 L11 12 13 若令, D=21 22 L23 ≠0 33 3 41n L13 11 av b D=b, 2 L23 D2=a21 b2 L23 D3= b L32 L33 a31 b 03 a31 an 可以验证,方程组有唯一解: D D, D; X2= D D D
对于三元线性方程组(1.2),若其系数行列式 D D x 1 1 = D D x 2 2 = = 1 12 13 1 22 23 2 3 32 33 a a D a b a a a b b = 11 13 2 21 23 1 2 31 33 3 a a D a a a b a b b = 11 12 3 21 22 31 3 2 2 1 3 b b a a D a a a b a D D x 3 3 = 可以验证,方程组有唯一解: 31 32 33 21 22 23 11 12 13 a a a a a a a a a 若令, D = 0

3.n阶行列式 对于n元线性方程组 41X1+412X2+L+41mxn=b1, azx1+az2x2+L +anxn=b2, (1.5) LLLLLLLLLLLLL amx+an2x+Lamxn=ba 定义记号: 0z1 L22 (1.6) M M MM An2 称为n阶行列式(简记为4(a,)
3.n阶行列式 对于n元线性方程组 . 11 1 12 2 1 21 1 22 2 2 2 1 1 2 2 n n n n n n nn n n a x a x a x b a x a x a x b a x a x a x b + = + = + = L L LLLLLLLLLLLLL L + + + + + + 1 , , (1.5) 定义记号: 称为n 阶行列式(简记为( ) aij )。 11 12 1 21 22 2 1 2 n n n n nn a a a a a a a a a L L M M M M L (1.6)