
二元线性方程组 411X1+a12x2=b 2IX1+422X2=b2 求解公式为 请观察,此公式有何特点? [=a2-6 >分子、分母均是两个数的乘积减去 411L22-412021 5-6-41 另外两个数的乘积 0112-012021
求解公式为 11 1 12 2 1 21 1 22 2 2 a x a x b a x a x b + = + = 1 22 12 2 1 11 22 12 21 11 2 1 21 2 11 22 12 21 b a a b x a a a a a b b a x a a a a − = − − = − 二元线性方程组 请观察,此公式有何特点? ➢分子、分母均是两个数的乘积减去 另外两个数的乘积
二元线性方程组 我们引进新的符号来表示“两个 数乘积减去另外两个数的乘积”。 12 数表 12 22 记号 求解公式为 2 22 b,42-42b2 D 2 =41122-41221 X1= 021 L22 L1122-12L21 表达式411422一称泡由该记号所确定的 411b2-b1421 二阶行列式(Determinant). 01122-01221 其中,4(i=1,2;j=1,2)称为元素. i为行标,表明元素位于第行; 为列标,表明元素位于第列
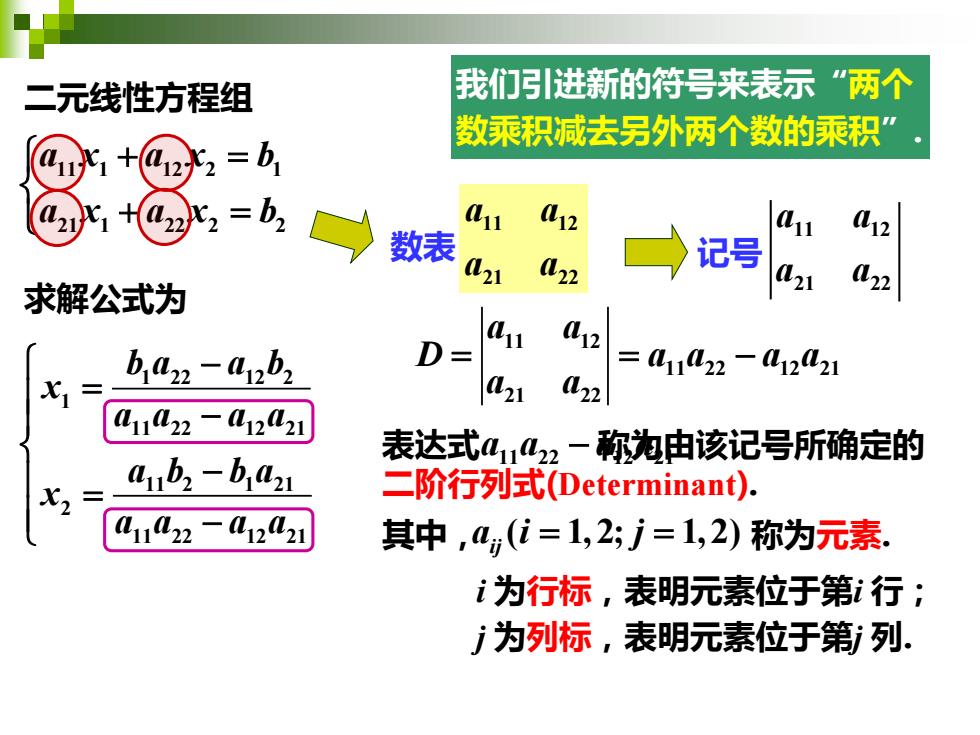
求解公式为 11 1 12 2 1 21 1 22 2 2 a x a x b a x a x b + = + = 1 22 12 2 1 11 22 12 21 11 2 1 21 2 11 22 12 21 b a a b x a a a a a b b a x a a a a − = − − = − 二元线性方程组 我们引进新的符号来表示“两个 数乘积减去另外两个数的乘积”. 11 12 11 22 12 21 21 22 a a D a a a a a a = = − 记号 11 12 21 22 a a a a 11 12 21 22 a a 数表 a a 表达式 称为由该记号所确定的 二阶行列式(Determinant). 11 22 12 21 a a a a − 其中, ( 1,2; 1,2) 称为元素. ij a i j = = i 为行标,表明元素位于第i 行; j 为列标,表明元素位于第j 列

注: ()二阶行列式 01 的值是由这四个元素所 L21 a22 表示的一个式子。 (2)记忆方法:对角线法则 主对角线上两元素之积一副对角线上两元素之积 主对角线 12 =011022-01221 副对角线 2 如 1×4-2×3=-2 3
注: (1) 二阶行列式 的值是由这四个元素所 表示的一个式子。 (2) 记忆方法:对角线法则 主对角线上两元素之积 - 副对角线上两元素之积 21 22 11 12 a a a a 11 12 21 22 a a a a 主对角线 11 22 = a a 12 21 −a a 副对角线 如: 1 2 3 4 = 1 4 − 2 3 = −2
二元线性方程组 (右端项) 若令 D= 12 ≠0(方程组的系数行列式) 21 2 b D1= 012 b, D2 L22 021 则上述二元线性方程组的解可表示为 七=642-44 01122-01221 41b2-b421 2= 01122-012021
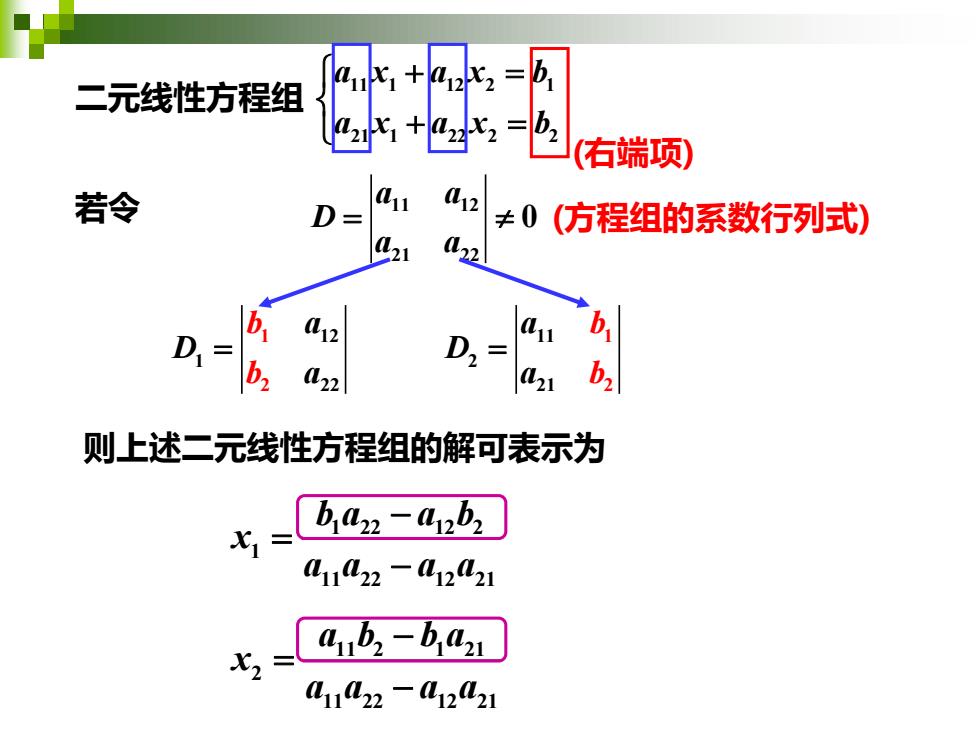
二元线性方程组 11 1 12 2 1 21 1 22 2 2 a x a x b a x a x b + = + = 若令 11 12 21 22 0 a a D a a = 12 1 1 2 22 b b a D a = 1 2 2 11 21 a b D a b = (方程组的系数行列式) 则上述二元线性方程组的解可表示为 1 22 12 2 1 1 11 22 12 21 D D b a a b x a a a a = − = − 11 2 1 21 2 2 11 22 12 21 a b b a D x a a a a D − = = − (右端项)

如:计算线性方程组 七1+2x2=3 2x1+3x2=4 则方程组的系数行列式D=】引 =1×3-2×2=-1≠0 .线性方程组有唯一的解 令: 则原线性方程组的解为 X1=-1,x2=2
如: 计算线性方程组 1 2 1 2 2 3 . 2 3 4 x x x x + = + = 则方程组的系数行列式 1 2 2 3 D = 1 3 2 4 3 D = 2 1 3 2 4 D = 则原线性方程组的解为 1 2 x x = − = 1, 2. = − 1 3 2 2 = − 1 0 线性方程组有唯一的解. 令: = 1, = -2