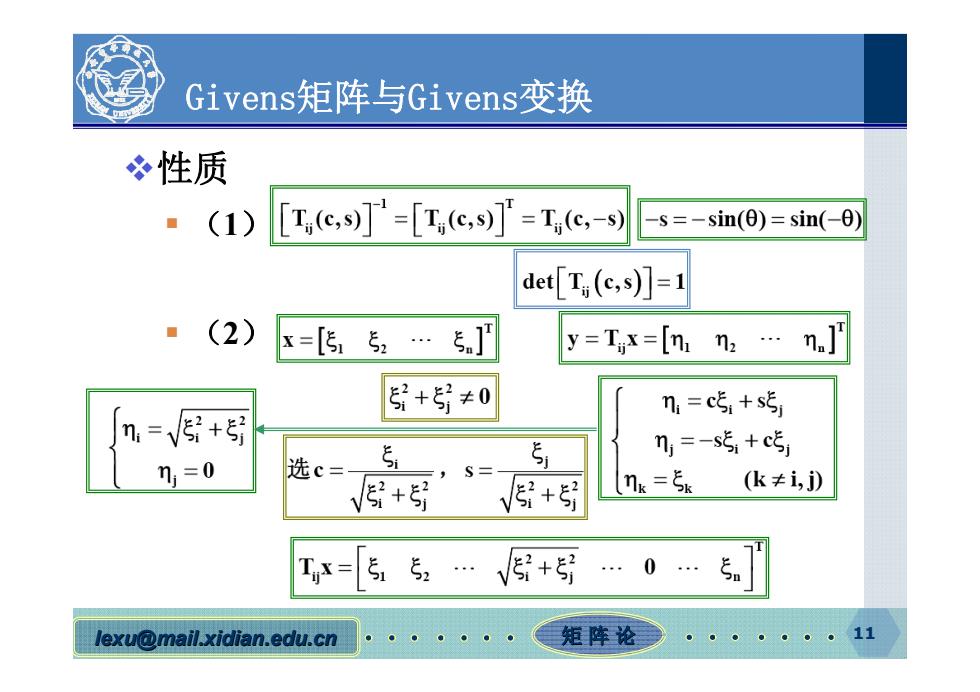
Givens?矩阵与Givens?变换 性质 ·(1) [,c,]'=[T,c,s]=工,c,-) s=-sin(θ)=sin(-0) det[T,(c,)]=1 (2) x=[5152… 57 y=Tx=[n1n2… +号≠0 n=c吃+s5, n=V贤+号 n=0 选c= 5 5 门=-s5+c5) S= V+号 V+另 nk =Ek (k≠i,j) Tx= …0… lexu@mail.xidian.edu.cn 矩阵论 11
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 11 Givens矩阵与Givens变换 性质 (1) (2)

Givens矩阵与Givens?变换 定理1. ▣设x=[552…5]'≠0 ·存在有限个Givens矩阵的乘积T,使得Tx=xe, 其中: ·x为实数时N=V=互 ·x为复数时 = ·e1=[100…0] lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 12 Givens矩阵与Givens变换 定理1. 设 存在有限个Givens矩阵的乘积T,使得 其中: • x为实数时 • x为复数时 • T 12 n x 0 Tx x e 1 2 T 2 x x xx H x xx T 1 e 100 0