西安电子科技大学：《矩阵论》研究生课程教学课件（讲义，2015）23 广义特征值与极小极大原理

矩阵论 主讲教师：徐乐 2015年1月13日星期二

2015年1月13日星期二 矩 阵 论 主讲教师：徐乐

上讲回顾 ÷第22讲矩阵特征值估计 ·特征值界的估计 ·盖尔圆法 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第22讲 矩阵特征值估计  特征值界的估计  盖尔圆法

特征值界的估计 冬矩阵特征值估计 ·特征值计算较困难，希望找到简便的特征值界 限或分布范围的估计方法 冬定理1 ·设A∈R×n,为A的任意特征值，则有 m()sx-D ·其中 M=max ai-ai 1Si,jSn 2 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 特征值界的估计 矩阵特征值估计  特征值计算较困难，希望找到简便的特征值界 限或分布范围的估计方法 定理1  设A∈Rn×n，λ为A的任意特征值，则有 • 其中   nn 1   Im M 2   ij ji 1 i,j n a a M max   2  

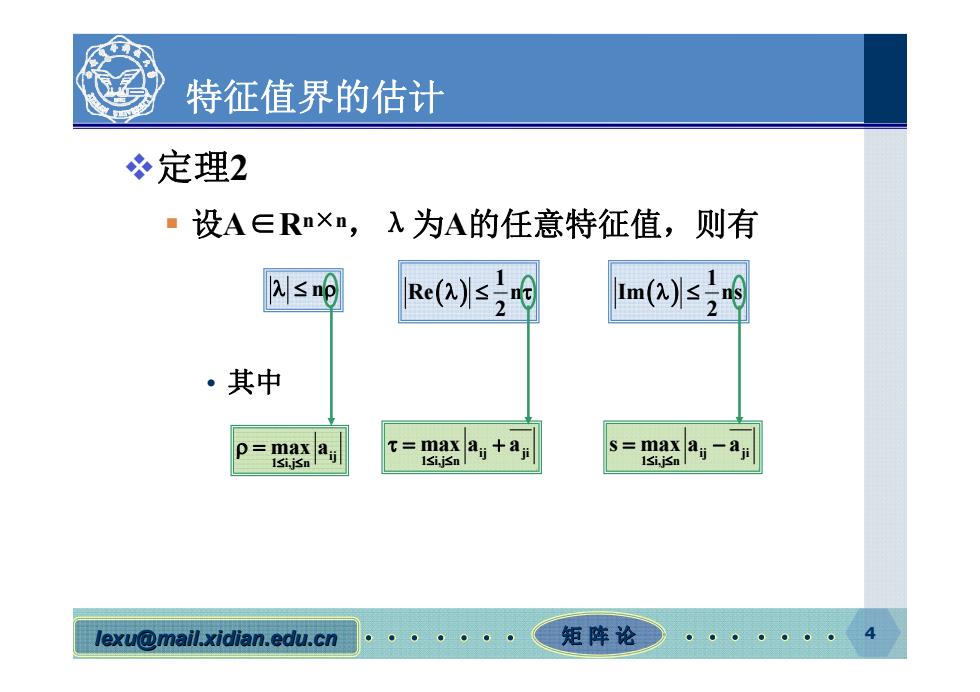
特征值界的估计 冬定理2 ·设A∈Rn×n,入为A的任意特征值，则有 ≤吗 Re()s Im(Z)s ·其中 p=maxa可 t=max ai +a s=max ai-aj 1si,jSn 1Si,jSn l 1si,iSn I lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 特征值界的估计 定理2  设A∈Rn×n，λ为A的任意特征值，则有 • 其中  n   1 Re n2      1 Im ns 2   ij 1 i,j n max a     ij ji 1 i,j n max a a     ij ji 1 i,j n s max a a    

盖尔圆法 必定义 ·设A=(anXn∈RnXn, 由方程所确定的圆称为A 的第个盖尔圆，R称为盖尔圆的半径 -R,=aol izi 定理3 ·矩阵A的所有特征值均落在它的所有盖尔圆的 并集之中 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 盖尔圆法 定义  设A=(ai,j)n×n∈Rn×n，由方程所确定的圆称为A 的第i个盖尔圆，Ri称为盖尔圆的半径 定理3  矩阵A的所有特征值均落在它的所有盖尔圆的 并集之中 n ii i ij j 1 i j za R a    