
IDIAN 131 UNIVE 矩阵论 主讲教师:徐乐 2015年1月13日星期二
2015年1月13日星期二 矩 阵 论 主讲教师:徐乐

上讲回顾 第21讲范数理论 范数理论及其应用 ·向量范数 ·矩阵范数 ·应用 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 2 上讲回顾 第21讲 范数理论 范数理论及其应用 • 向量范数 • 矩阵范数 • 应用

向量范数 冬向量范数定义 ·设V为数域K上的向量空间,若对于V的任一向 量x,对应一个实值函数x,并满足以下三个 条件 ·非负性x≥0,等号当且仅当x=0时成立; ·齐次性lax=x,a∈k,x∈V; ·三角不等式k+y≤x+y,x,y∈V ·则称x为V中向量x的范数,简称为向量范数 2s[2[2) H6lder不等式 P,q>1,-+-=1,a,b>0 lexu@mail.xidian.edu.cn 8●●
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 3 向量范数 向量范数定义 设V为数域K上的向量空间,若对于V的任一向 量x,对应一个实值函数||x||,并满足以下三个 条件 • 非负性||x||≥0,等号当且仅当x=0时成立; • 齐次性 • 三角不等式 则称||x||为V中向量x的范数,简称为向量范数 x x , k,x V; x y x y ,x,y V 1 1 n nn p q p q ii i i i1 i1 i1 i i ab a b 1 1 p,q 1, 1,a ,b 0 p q Hölder不等式
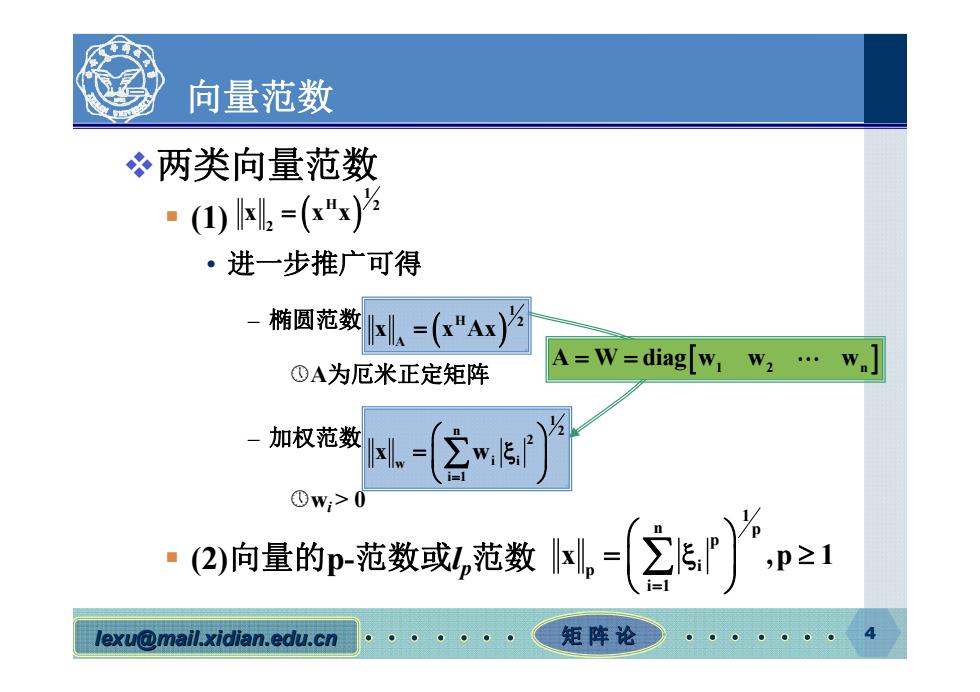
向量范数 冬两类向量范数 ·()6=x) ·进一步推广可得 椭圆范数,=(”Ax OA为厄米正定矩阵 A=W=diag[w1w2…w。 -加权范数 0w,>0 ·2向蚕的即-格数范数风-(②产p1 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 4 向量范数 两类向量范数 (1) • 进一步推广可得 – 椭圆范数 A为厄米正定矩阵 – 加权范数 wi > 0 (2)向量的p-范数或lp范数 1 H 2 2 x xx 1 H 2 A x x Ax 1 n 2 2 w i i i 1 x w A W diag w w w 12 n 1 n p p p i i 1 x ,p 1

向量范数 冬向量范数的等价性 ·定理1 ·设l。、lB为C的两种向量范数 ·则必定存在正数m、M(m、M与x无关),使得 mlxa≤ke≤Mla ·它就称为向量范数的等价性 ·同时有 sN.s。 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 5 向量范数 向量范数的等价性 定理1 • 设||●||α、||●||β为Cn的两种向量范数 • 则必定存在正数m、M (m、M与x无关) ,使得 • 它就称为向量范数的等价性 同时有 mx x Mx 1 1 xx x M m