西安电子科技大学：《矩阵论》研究生课程教学课件（讲义，2014）12 矩阵的QR分解

其他三角分解 定义设A具有唯一的LDU分解 ·A的Doolittle分解 ·将D,U结合起来得A=LU(U=DU) ·A的Crout2分解 ·将L,D结合起来得A=L(L=LD) 冬厄米正定矩阵的Cholesky2分解 A=GGH lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 其他三角分解 定义 设A具有唯一的LDU分解  A的Doolittle分解 •  A的Crout分解 • 厄米正定矩阵的Cholesky分解  H A GG 

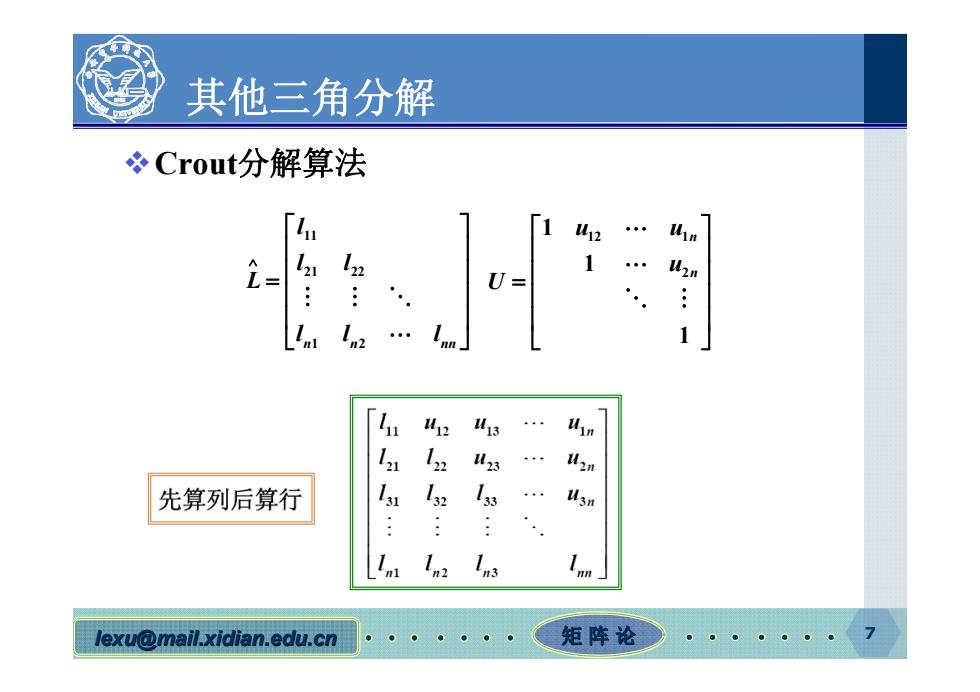
其他三角分解 冬Crout分解算法 「1 412 2= 21 U= 42 3 12 423 先算列后算行 132 43n 1n2 lexu@mail.xidian.edu.cn 矩阵论●

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 其他三角分解 Crout分解算法 7 11 21 22 n n nn 1 2 l l l L ll l                 12 1 2 1 1 1 n n u u u U                 

第12讲矩阵的QR分解 Givens矩阵与Givens7变换 冬Householder矩阵与Householder变换 QR分解 lexu@mail.xidian.edu.cn 矩阵论●

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 第12讲 矩阵的QR分解 Givens矩阵与Givens变换 Householder矩阵与Householder变换 QR分解

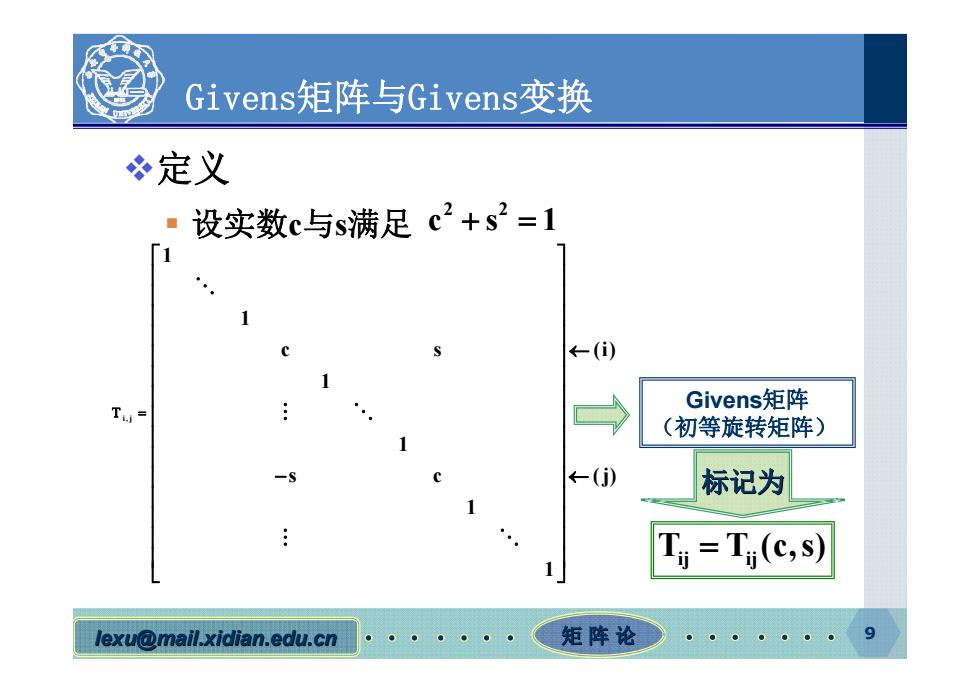
Givens矩阵与Givens变换 必定义 设实数c与s满足c2+s2=1 ←(i) T= 〉 Givens矩阵 (初等旋转矩阵) ←() 标记为 Tj=Tj(c,s) lexu@mail.xidian.edu.cn 矩阵论

lexu @mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 Givens矩阵与Givens变换 定义  设实数 c 与 s满足 2 2 cs1   i,j 1 1 c s (i) 1 1 s c ( j) 1 1                                             Givens矩阵 （初等旋转矩阵） T T (c,s) ij ij  标记为

Givens矩阵与Givens?变换 由Givens矩阵所确定的线性变换称为Givens 变换 ■亦称初等旋转变换 ·Notel:存在0，使得c=cos(O),s=sin(θ) ■Note2:平面直角坐标系中绕原点旋转0变换 cos(0) sin(0) y= -sin(0) cos(0) ▣Note3: 实Givens矩阵可推广为复初等旋转矩阵 lexu@mail.xidian.edu.cn 矩阵论 10

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 10 Givens矩阵与Givens变换 由Givens矩阵所确定的线性变换称为Givens 变换  亦称初等旋转变换  Note1：存在θ，使得  Note2：平面直角坐标系中绕原点旋转θ变换  Note3：实Givens矩阵可推广为复初等旋转矩阵 c cos( ),s sin( )    cos( ) sin( ) y x sin( ) cos( )          