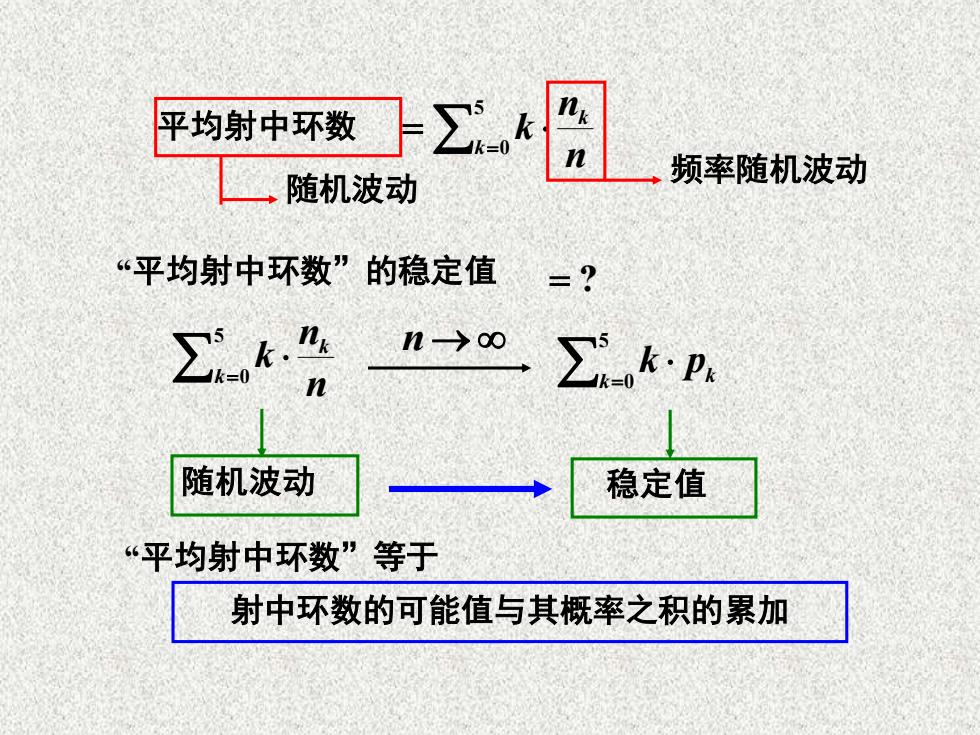
平均射中环数 ∑k n 随机波动 频率随机波动 “平均射中环数”的稳定值 =? ∑k n→o, n ∑kp 随机波动 稳定值 “平均射中环数”等于 射中环数的可能值与其概率之积的累加
= = 5 k 0 k n n 平均射中环数 k 频率随机波动 随机波动 = 5 k 0 k n n k n → = 5 k 0 k pk 随机波动 稳定值 “平均射中环数”的稳定值 = ? “平均射中环数”等于 射中环数的可能值与其概率之积的累加

分赌本问题 A期望所得的赌金即为X的数学期望 3 E(X)=200×+0×,=150(元), 4 射击问题 “平均射中环数”应为随机变量Y的数学期望 E(Y)= 0×P+1×p1+2×P2+3×P3+4×P4+5×ps:
分赌本问题 A 期望所得的赌金即为X 的数学期望 射击问题 “平均射中环数”应为随机变量Y 的数学期望 0 1 2 3 4 5 . ( ) p0 p1 p2 p3 p4 p5 E Y + + + + + = 150( ). 4 1 0 4 3 E(X) = 200 + = 元

2、离散型随机变量的数学期望 定义设离散型随机变量X的分布律为 P(X=x)=pk,k=1,2,:. 若级数∑xP4绝对收敛则称级数∑xP k=1 的和为随机变量X的数学期望记为E(X).即 E(X)=
定义 ( ) . , ( ). , { } , 1,2, . 1 1 1 = = = = = = = k k k k k k k k k k k E X x p X E X x p x p P X x p k X 的和为随机变量 的数学期望 记 为 即 若级数 绝对收敛 则称级数 设离散型随机变量 的分布律为 2、离散型随机变量的数学期望

关于定义的几点说明 (1)E(X)是一个实数,而非变量,它是一种加 权平均,与一般的平均值不同,它从本质上体现 了随机变量X取可能值的真正的平均值,也称 均值. (2)级数的绝对收敛性保证了级数的和不 随级数各项次序的改变而改变,之所以这样要 求是因为数学期望是反映随机变量X取可能值 的平均值,它不应随可能值的排列次序而改变 (3)随机变量的数学期望与一般变量的算 术平均值不同
关于定义的几点说明 (3) 随机变量的数学期望与一般变量的算 术平均值不同. (1) E(X)是一个实数,而非变量,它是一种加 权平均,与一般的平均值不同, 它从本质上体现 了随机变量X 取可能值的真正的平均值, 也称 均值. (2) 级数的绝对收敛性保证了级数的和不 随级数各项次序的改变而改变, 之所以这样要 求是因为数学期望是反映随机变量X 取可能值 的平均值,它不应随可能值的排列次序而改变

1 2 假设 卫 0.020.98 随机变量X的算术平均值为 1+2 =1.5, 2 E(X)=1×0.02+2×0.98=1.98. X 1 它从本质上体现了随机变量X取可能值的平均值 当随机变量X取各个可能值是等概率分布时,X 的期望值与算术平均值相等
随机变量 X 的算术平均值为 1.5, 2 1 2 = + 假设 E(X) = 1 0.02 + 2 0.98= 1.98. 它从本质上体现了随机变量X 取可能值的平均值. 当随机变量X 取各个可能值是等概率分布时, X 的期望值与算术平均值相等. x O • • 1 • 2 • • X 1 2 p 0.02 0.98