
第三节1 随机变量的分布函数 一分布函数的概念 二.分布函数的性质 重点:求分布函数; 用概率分布计算有关事件的概率
一.分布函数的概念 二.分布函数的性质 重点: 求分布函数; 第三节 随机变量的分布函数 用概率分布计算有关事件的概率

对于离散型随机变量X P{X=xx}=p,k=1,2, 或 X X2 X3 。 p P P2 P3 利用分布律描述 问题: 非离散型随机变量 ?? PIX=a)-0,VaER
{ } , , , 1 2 P X x p k = = = k k 对于离散型随机变量 X 问题: 非离散型随机变量 1 2 3 1 2 3 X x x x p p p p 或 ?? 利用分布律描述 P X a a R { } 0, = =
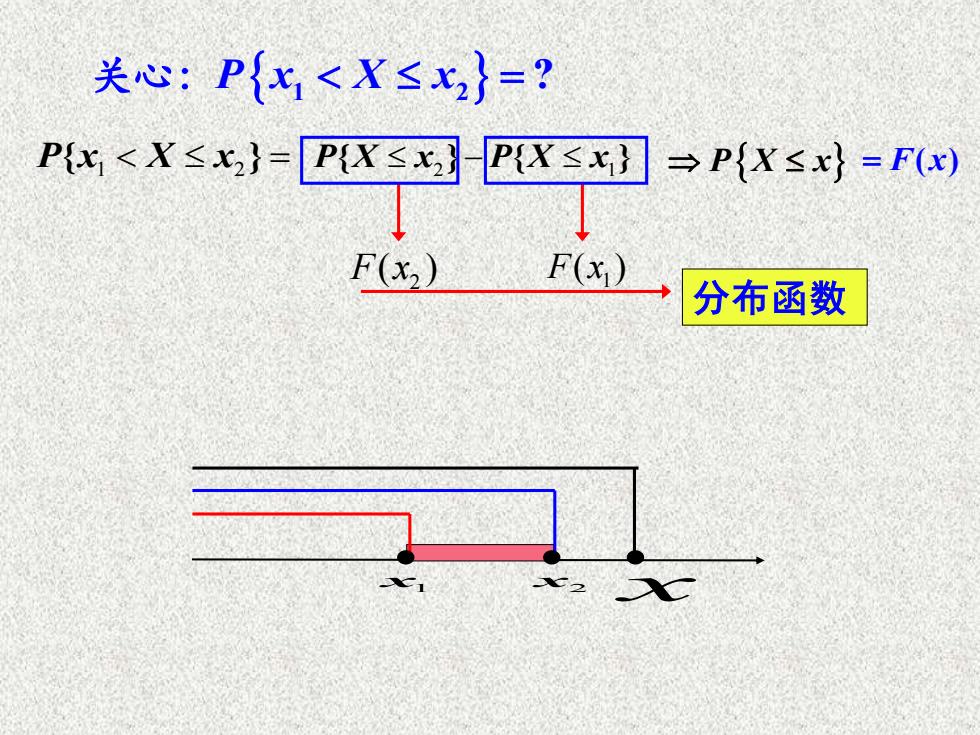
关心:P{x<X≤,}=? Px<X≤x,}=P(XsxP(X]→P{X≤}=Fw) F(x2) F(x) 分布函数
P x X x { } 1 2 = − 2 1 P X x P X x { } { } 2 F x( ) 1 F x( ) 分布函数 x1 x2 x 关心:P x X x 1 2 = ? P X x = F x( )

一、分布函数的概念 定义设X是一个随机变量,x是任意实数,函数 F(x)=P{X≤x} 称为X的分布函数.(Distribution Functior) 说明: (I)分布函数F(x)是x的普通实函数, 定义域(-∞,o);对应法则:F(x)=P{X≤x} (2)Fx)反映随机变量取值X≤x的概率,故又称累计概率 函数
, ( ) { . , } X x F x X x X = P 定义 设 是一个随机变量 是任意实数 函数 称为 的分布函数 一、分布函数的概念 (Distribution Function) 说明: (2) F(x)反映随机变量取值X ≤x的概率,故又称累计概率 函数. (1) ( ) : (x) { } F x x 定义 − F P X x = 分布函数 是 的普通实函数, 域( , );对应法则

说明: (3)随机变量X落在任一区间(x1,x2】]上的概率 P{x1<X≤x2}=P{X≤x2}-P{X≤x1}=F(x2)-F(x). 即,Fx)完整地描述了随机变量的统计规律性
1 2 P x X x { } 2 1 = − P X x P X x { } { } 2 1 = − F x F x ( ) ( ). 1 2 (3)随机变量 X x x 落在任一区间( , ]上的概率 x X o 1 x 2 x 即,F(x)完整地描述了随机变量的统计规律性。 说明: