
数学建模与数学实验 tw 线性规划
线性规划 数学建模与数学实验

实验目的 1.了解线性规划的基本内容 2.掌握用数学软件包求解线性规划问题 实验内容 1.两个引例 2.用数学软件包MATLAB:求解线性规划问题. 3.用数学软件包LINDO、LNGO求解线性规划问题. 4.建模案例:投资的收益与风险. 5.实验作业
实验目的 实验内容 2. 掌握用数学软件包求解线性规划问题. 1. 了解线性规划的基本内容. 2. 用数学软件包MATLAB求解线性规划问题. 5. 实验作业. 3. 用数学软件包LINDO、LINGO求解线性规划问题. 1. 两个引例. 4. 建模案例:投资的收益与风险
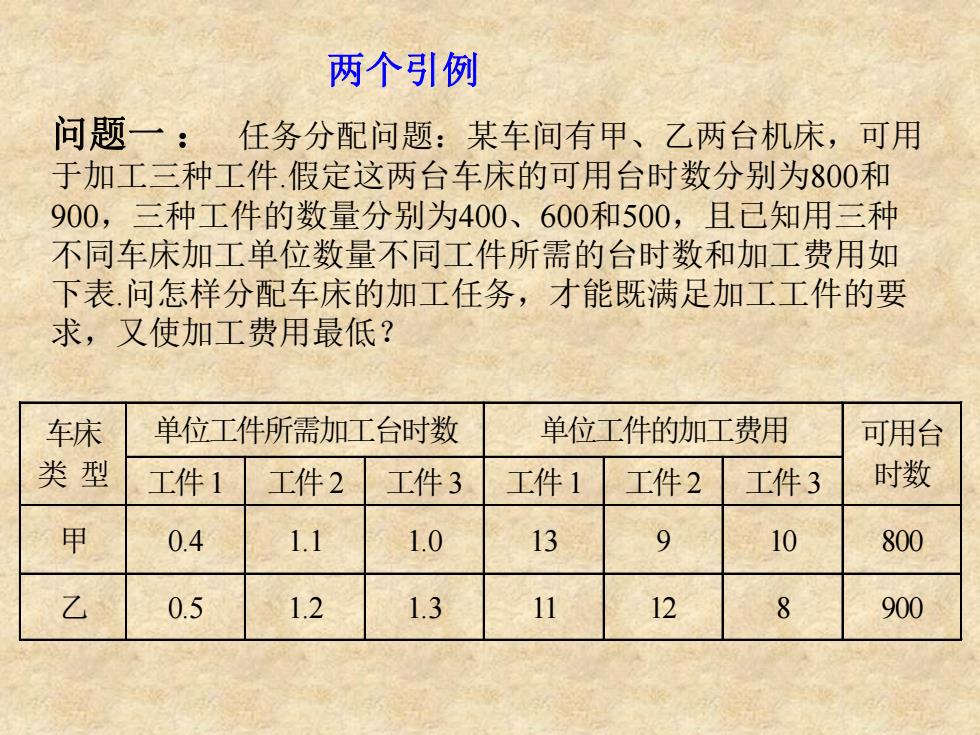
两个引例 问题一:任务分配问题:某车间有甲、乙两台机床,可用 于加工三种工件.假定这两台车床的可用台时数分别为800和 900,三种工件的数量分别为400、600和500,且已知用三种 不同车床加工单位数量不同工件所需的台时数和加工费用如 下表问怎样分配车床的加工任务,才能既满足加工工件的要 求,又使加工费用最低? 车床 单位工件所需加工台时数 单位工件的加工费用 可用台 类型 工件1 工件2 工件3 工件1 工件2 工件3 时数 甲 0.4 1.1 1.0 13 9 10 800 乙 0.5 1.2 1.3 11 12 8 900
问题一 : 任务分配问题:某车间有甲、乙两台机床,可用 于加工三种工件.假定这两台车床的可用台时数分别为800和 900,三种工件的数量分别为400、600和500,且已知用三种 不同车床加工单位数量不同工件所需的台时数和加工费用如 下表.问怎样分配车床的加工任务,才能既满足加工工件的要 求,又使加工费用最低? 车床 单位工件所需加工台时数 单位工件的加工费用 类 型 工件1 工件2 工件3 工件1 工件2 工件3 可用台 时数 甲 0.4 1.1 1.0 13 9 10 800 乙 0.5 1.2 1.3 11 12 8 900 两个引例

解设在甲车床上加工工件1、2、3的数量分别为x1、2、x, 在乙车床上加工工件1、2、3的数量分别为x4、x5、x6,可建立以 下线性规划模型: minz=13x1+9x2+10x3+11x4+12x5+8x6 X1+x4=400 x2+x=600 x3+x.=500 S.t. 0.4x+1.1x2+x3≤800 0.5x4+1.2x+1.3x6≤900 x,≥0,i=1,2,.,6 解签
解 设在甲车床上加工工件1、2、3的数量分别为x1、x2、x3, 在乙车床上加工工件1、2、3的数量分别为x4、x5、x6 ,可建立以 下线性规划模型: 解答

问题二:某厂每日8小时的产量不低于1800件.为了进行质量 控制,计划聘请两种不同水平的检验员.一级检验员的标准为: 速度25件/小时,正确率98%,计时工资4元/小时:二级检验员 的标准为:速度15件/小时,正确率95%,计时工资3元/小时.检 验员每错检一次,工厂要损失2元.为使总检验费用最省,该工 厂应聘一级、二级检验员各几名? 解设需要一级和二级检验员的人数分别为x1、x2人, 则应付检验员的工资为: 8×4×x+8×3×x2=32x,+24x2 因检验员错检而造成的损失为: (8×25×2%×x+8×15×5%×x2)×2=8x,+12x2
问题二: 某厂每日8小时的产量不低于1800件.为了进行质量 控制,计划聘请两种不同水平的检验员.一级检验员的标准为: 速度25件/小时,正确率98%,计时工资4元/小时;二级检验员 的标准为:速度15件/小时,正确率95%,计时工资3元/小时.检 验员每错检一次,工厂要损失2元.为使总检验费用最省,该工 厂应聘一级、二级检验员各几名? 解 设需要一级和二级检验员的人数分别为x1、x2人, 则应付检验员的工资为: 1 2 1 2 8 4 x 8 3 x 32x 24x 因检验员错检而造成的损失为: 1 2 2 8 1 12 2 (8 25 2% x 8155% x ) x x