
上节内容回顾 一、分布函数的概念 定义设X是一个随机变量,x是任意实数,函数 F(x)=P{X≤x}称为X的分布函数. 定义域(一∞,0) 二、分布函数的性质 (1)F(x)是一个不减函数 (2)0≤F(x)≤1,且 F(-oo)=lim F(x)=0 F(oo)=lim F(x)=1. x00 00 (3)F(x)处处右连续. 即limF(x)=F(xo),(-oo<x。<oo)
一、分布函数的概念 二、分布函数的性质 上节内容回顾 定义域(− , ) ( ) lim ( ) 1. x F F x → = = (2 0 ( ) 1 ) F x ,且 (1 ( ) )F x 是一个不减函数. ( ) lim ( ) 0 x F F x →− − = = (3 ( ) )F x 处处右连续. 0 0 0 lim ( ) ( ), ( ). x x F x F x x → + 即 = − , , ( ) { } . X x F x P X x X = 定义 设 是一个随机变量 是任意实数 函数 称为 的分布函数

“离散型随机变量分布律与分布函数的关系” 分布律 Pk=P{X=x},k=1,2,. 分布函数F(x)=PX≤x=∑PX=x=∑P:(x∈R) xASx xRSx 离散型随机变量分布函数Fx)在x=x(k=1,2,.)处有跳 跃,其跳跃值为P=PX=x. 0,x<-1, ↑F(x) 1-4 1 -1≤x<2, F(x)= 4 2≤x<3, 1, x≥3. -10 23
分布函数 F x P X x ( ) { } = 分布律 { }, 1,2, . . k k p P X x k = = = “离散型随机变量分布律与分布函数的关系” ( x∈R ) { } k k k k x x x x P X x p = = = 离散型随机变量分布函数F (x) 在 x = xk (k =1, 2 ,.) 处有跳 跃,其跳跃值为 pk=P{X= xk }. o x F(x) 1 -1 2 3 0, 1, 1 , 1 2, 4 ( ) 3 , 2 3, 4 1, 3. x x F x x x − − =

例2一个靶子是半径为2米的圆盘,设击中靶上任一同心圆盘上 的点的概率与该圆盘的面积成正比,并设射击都能中靶,以X表 示弹着点与圆心的距离.试求随机变量X的分布函数. 解1)x<0时,F(x)=P{X≤x}=0: 2)0≤x≤2时, F(x)=P{X≤x}=P{X<O}+P{0≤X≤x} P{0≤X≤x}=x2,k是常数.取x=2, P0≤X≤2=l,得4=1,因而P0≤xs= 41 Fg=PX≤=Px<+P0sX≤=
例2 一个靶子是半径为2米的圆盘,设击中靶上任一同心圆盘上 的点的概率与该圆盘的面积成正比, 并设射击都能中靶, 以X表 示弹着点与圆心的距离. 试求随机变量 X 的分布函数. 解 1) 0 , x 时 2) 0 2 , x 时 2 P X x kx k {0 } , . = 是常数 由P X {0 2} 1, = 得 4 1, k = 2 {0 } . 4 x 因而P X x = F x P X x ( ) { } 0; = = = F x P X x ( ) { }= P X{ 0}+ P X x {0 } 2 . 4 x = F x P X x ( ) { } = = P X{ 0} + P X x {0 } 取 x =2
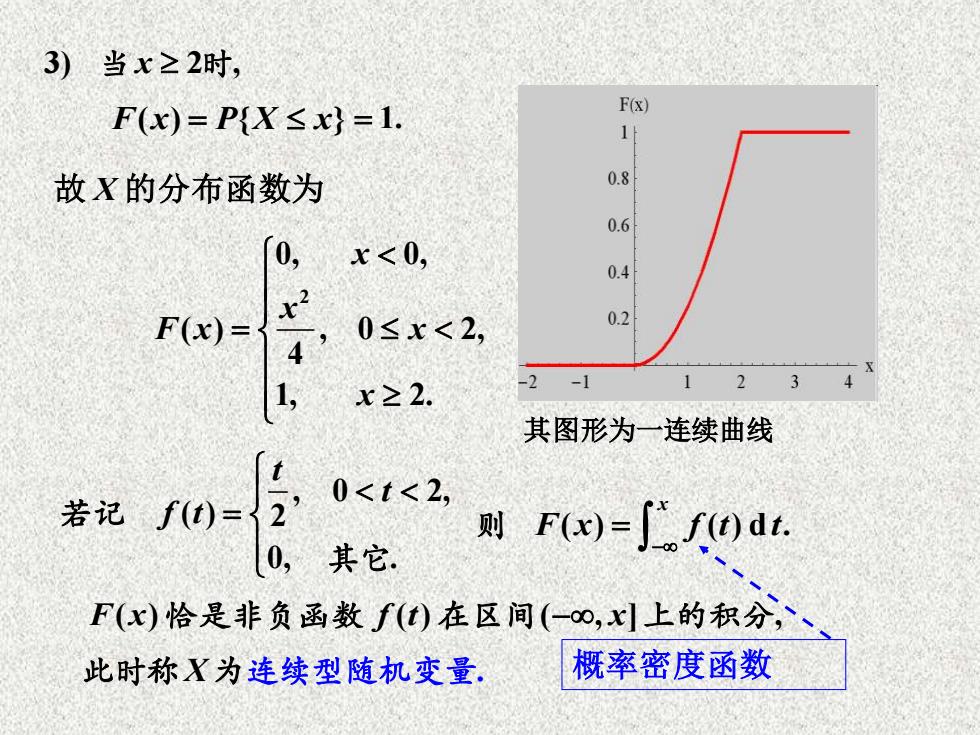
3)当≥2时, F(x)=P{X≤x}=1. F(x) 1 故X的分布函数为 0.8 0.6 0, x<0, 0.4 F(x)= 0≤x<2, 0.2 4 x≥2. -2 -1 2 其图形为一连续曲线 0<t<2, 则F()=」f)dt. 0,其它 F(x)恰是非负函数f(t)在区间(一o,x上的积分,、 此时称X为连续型随机变量 概率密度函数
3) 2 , 当 x 时 故 X 的分布函数为 2 0, 0, ( ) , 0 2, 4 1, 2. x x F x x x = F x P X x ( ) { } = = 1. 其图形为一连续曲线 , 0 2, ( ) 2 0, . t t f t = 若记 其它 ( ) ( ) d . x F x f t t − = 则 F x f t x ( ) ( ) ( , ] , 恰是非负函数 在区间 − 上的积分 此时称 X为连续型随机变量. 概率密度函数

第四节连续型随机变量及其概率密度 一、连续型随机变量及其 概率密度的概念与性质 二、常见连续型随机变量的分布
一、连续型随机变量及其 概率密度的概念与性质 二、常见连续型随机变量的分布 第四节 连续型随机变量及其概率密度