
分析假设继续赌两局,则结果有以下四种情况: AA AB BA BB A胜B负 A胜B负 B胜A负 B胜A负 A胜B负 B胜A负 A胜B负 B胜A负 把已赌过的三局(A胜2局、B胜1局)与上述结果 相结合,即A、B赌完五局: 前三局 A胜2局B胜1局 后二局: AA AB BA BB A胜 B胜
前三局: A胜2局B胜1局 后二局: 把已赌过的三局(A 胜2局、B 胜1局)与上述结果 相结合, 即A、B赌完五局: A A A B B A B B A胜 B胜 分析 假设继续赌两局, 则结果有以下四种情况: A A A B B A B B A胜B负 A胜B负 A胜B负 B胜A负 B胜A负 A胜B负 B胜A负 B胜A负

故有,在赌技相同的情况下,A、B最终获胜的 可能性大小之比为3:1. 即A应获得赌金的,而B只能获得赌金的 因此,A能“期望”得到的数目应为 20子+0x150元 4 而B能“期望”得到的数目,则为 20×}+0=5元
因此, A 能“期望”得到的数目应为 4 1 0 4 3 200 + = 150(元), 而B 能“期望”得到的数目, 则为 4 3 0 4 1 200 + = 50(元). 故有, 在赌技相同的情况下, A、B最终获胜的 可能性大小之比为 3:1. 即A 应获得赌金的 , 而 B 只能获得赌金的 4 3 . 4 1

若设随机变量X为在A胜2局B胜1局的前提 下,继续赌下去A最终所得的赌金。 则X所取可能值为: 200 0 3 1 其概率分别为: 4 4 因而A期望所得的赌金即为X的“期望”值, 等于 20<+0×元 即为的可能值与其概率之积的累加
因而A期望所得的赌金即为X的 “期望”值, 等于 X的可能值与其概率之积的累加. 150( ). 4 1 0 4 3 200 + = 元 即为 若设随机变量 X 为在 A 胜2局B 胜1局的前提 下, 继续赌下去 A 最终所得的赌金. 则X 所取可能值为: 200 0 其概率分别为: 4 3 4 1
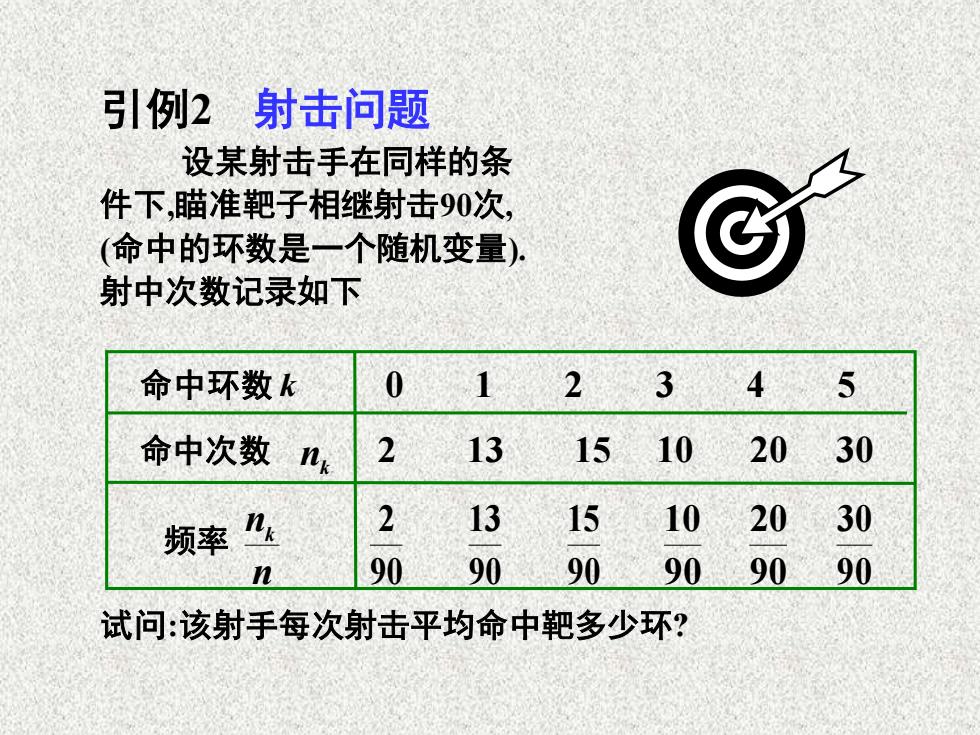
引例2射击问题 设某射击手在同样的条 件下,瞄准靶子相继射击90次, (命中的环数是一个随机变量). 射中次数记录如下 命中环数k 0 123 4 5 命中次数 2 13151020 30 频率 2 131510 2030 L 90 9090 90 90 90 试问:该射手每次射击平均命中靶多少环?
设某射击手在同样的条 件下,瞄准靶子相继射击90次, (命中的环数是一个随机变量). 射中次数记录如下 引例2 射击问题 试问:该射手每次射击平均命中靶多少环? 0 1 2 3 4 5 2 13 15 10 20 30 90 15 90 13 90 2 90 20 90 10 90 30 命中环数 k 命中次数 频率 nk n nk

解 平均射中环数 。 射中靶的总环数 射击次数 =0×2+1x13+2×15+3×10+4×20+5×30 90 2,13.、15.210,20 =0× -+1× +2× +3× +4× 9090 90 9090 30 +5× 90 -∑k.-3.37 n 设射手命中的环数为随机变量Y
解 平均射中环数 射击次数 射中靶的总环数 = 90 0 2 + 113 + 215 + 310 + 4 20 + 5 30 = 90 30 5 90 20 4 90 10 3 90 15 2 90 13 1 90 2 0 + = + + + + = 3.37. = = 5 k 0 k n n k 设射手命中的环数为随机变量Y