(二)连续型随机变量的数学期望 1.问题的提出 设X是连续型随机变量,其密度函数为fx,取很密的分点x。<x<x2<. 由于x,与x#1很接近,所以区间x+)中的值可以用x,来近似代替 X落在小区间xx)的概率是[f(x)dx=f(x)x.-)=f(x)A 因此X与以概率f(x:)△x,取值x,的离散型随机变量近似, 该离散型随机变量的数学期望 ∑xfx:)Ag 正是广xfx)的渐近和式 小区间Kx+)
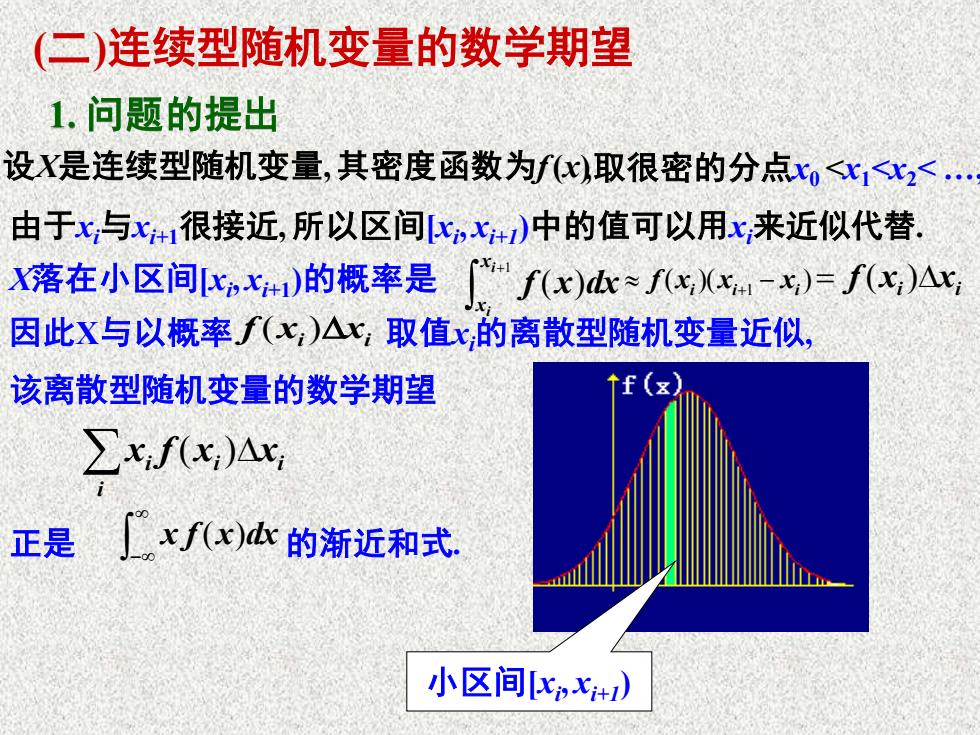
(二)连续型随机变量的数学期望 设X是连续型随机变量,其密度函数为f (x) +1 ( ) i i x x f x dx xi xi = f ( ) 小区间[xi , xi+1) ( )( ) xi xi 1 xi f + − 1. 问题的提出 X落在小区间[xi , xi+1)的概率是 ,取很密的分点x0 <x1<x2< ., 由于xi与xi+1很接近, 所以区间[xi , xi+1)中的值可以用xi来近似代替. xi xi 因此X与以概率 f ( ) 取值xi的离散型随机变量近似, 该离散型随机变量的数学期望 i i xi xi x f ( ) 正是 − x f (x)dx 的渐近和式

2.连续型随机变量数学期望 设连续型随机变量X的概率密度为f(x),若积分 ∫」xfx)dx绝对收敛,则称积分∫xfx)dx的值为 随机变量X的数学期望,记为E(X).即 E(X)=∫xf)dx 数学期望简称期望,又称为均值.又称某一分布的数学期望
2. 连续型随机变量数学期望 ( ) ( )d ( )d ( ). 设连续型随机变量 的概率密度为 ,若积分 绝对收敛,则称积分 的值为 随机变量 的数学期望,记为 即 X f x x f x x x f x x X E X − − 数学期望简称期望,又称为均值. 又称某一分布的数学期望. E X x f x x ( ) ( )d . − =

3.数学期望不存在的实例:柯西分布 X服从柯西分布,其密度函数为 f(x)= π(1+x2)” 由a4时-6 n+。a 因而其数学期望EX)不存在
由于 X服从柯西分布, 其密度函数为 ( ) ( ) , π 1 1 2 x f x + = ( ) ( ) ( ) 2 2 0 2 d 1 π 1 1 d π 1 1 x x x x x + + = + + + − = + = + 0 ln 1 π 1 2 x 因而其数学期望E(X)不存在. 3. 数学期望不存在的实例:柯西分布

二、常见分布的数学期望 1°若X服从参数为p的0-1)分布,则EX)=p。 2°若Xb(n,p),则EX=p. 证:EW-2Px=好-2Cpg -cdr Gic ∑nCp'qA -nCA-in-gt-np
二、常见分布的数学期望 证: 1º 若 X 服从参数为 p 的(0-1)分布,则 E(X)=p。 2º 若 X~b(n, p),则 E(X)=np. E X( ) 1 1 1 n k k n k n k nC p q − − − = 0 n k k n k n k kC p q − = = 1 n k k n k n k kC p q − = = 1 1 1 1 n k k n k n k np C p q − − − − = = = np. 0 { } n k kP X k = = = 1 1 k k n n n C C k − − =