
第二章随机变量及其分布 第一节随机变量 一、随机变量的引入 二、随机变量的概念 重点:随机变量的概念
二、随机变量的概念 一、随机变量的引入 第二章 随机变量及其分布 第一节 随机变量 重点:随机变量的概念
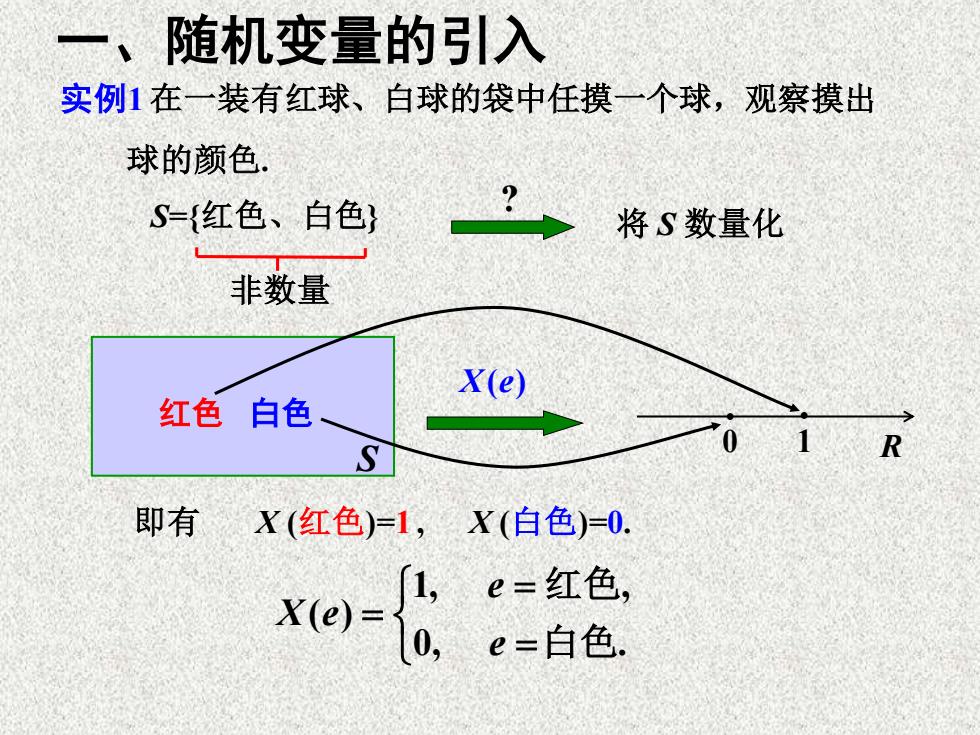
一、随机变量的引入 实例1在一装有红球、白球的袋中任摸一个球,观察摸出 球的颜色. S={红色、白色} 将S数量化 非数量 X(e) 红色白色 0 S R 即有 X(红色)=1,X(白色)=0 i-B e=红色, e=白色
实例1 在一装有红球、白球的袋中任摸一个球,观察摸出 球的颜色. S={红色、白色} 非数量 将 S 数量化 ? S 红色 白色 X e( ) 1 R • 0 • 即有 X (红色)=1 , = = = 0, . 1, , ( ) 白色 红色 e e X e X (白色)=0. 一、随机变量的引入

1.为什么引入随机变量? 概率论是从数量上来研究随机现象内在规律 性的,为了更方便有力的研究随机现象,就要用数学 分析(高等数学)的方法来研究,因此为了便于数 学上的推导和计算,就需将任意的随机事件数量化, 当把一些非数量表示的随机事件用数字来表示时, 就建立起了随机变量的概念
概率论是从数量上来研究随机现象内在规律 性的,为了更方便有力的研究随机现象,就要用数学 分析(高等数学)的方法来研究, 因此为了便于数 学上的推导和计算,就需将任意的随机事件数量化, 当把一些非数量表示的随机事件用数字来表示时, 就建立起了随机变量的概念. 1. 为什么引入随机变量?

2.随机变量(random variable)的引入 将形形色色的样本空间S中的元素e与实数x对应 起来,从而可用微积分方法研究。 问题:若记样本空间S={}(e表示样本空间的元素), 如何寻找一个规则X,将S的每个元素与实数x对应起来. 即 VeeS,e规则x→xeR 记作:X=X(e)一随机变量
——将形形色色的样本空间 S 中的元素 e 与实数 x 对应 起来,从而可用微积分方法研究。 2.随机变量(random variable)的引入 若记样本空间 ( 表示样本空间的元素), 如何寻找一个规则 ,将 的每个元素 与实数 对应起来 即 问题: { } . S e e X S e x = e S, 记作:X X e = ( ) 规则 X e x R ⎯⎯⎯→ —— 随机变量
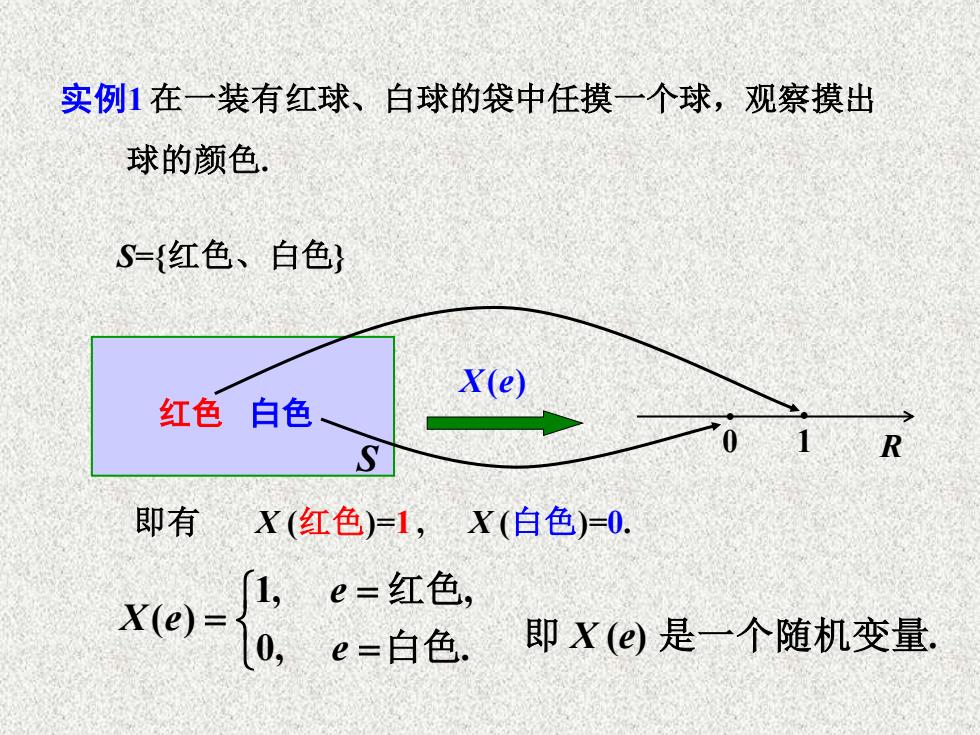
实例1在一装有红球、白球的袋中任摸一个球,观察摸出 球的颜色. S={红色、白色} X(e) 红色白色 S R 即有 X(红色)=1,X(白色)=0. e6&百6 即X(e是一个随机变量
实例1 在一装有红球、白球的袋中任摸一个球,观察摸出 球的颜色. S={红色、白色} S 红色 白色 X e( ) 1 R • 0 • 即有 X (红色)=1 , = = = 0, . 1, , ( ) 白色 红色 e e X e X (白色)=0. 即 X (e) 是一个随机变量