
第一章概率论的基本概念 来量生尺,粉察仅漏,目尽毛里,白菊暴策 —冲之 圈导学 —《便率论》在《桑合论》的善地上立足 更加复杂的计算工作,得请《微积分》出山,干是有了第二,三、四和五章, 全查可用一句话作为红线申起来, 随事件发生的可能性大小的定义及计的公潭化】 [1]随机率件,定义它为随机杖验£的若干个可能的结果构成的集合,即S 在学4个关系”3个运算时,要抓住图形,在A一B=A一AB,在数 写”《个律”时,重点是菌·章根律。 学会用字每表示事件,是一个重要的入门点,此关套过不可,香则,对习题 将桌手无 [2]麦生,试酸站果出来了,当且仅这一结果黑于A,则称事件A发生了, 典型情误:认为A发生是指A的所有元素均在试验结果中同时出现,若忽视了 这个餐色,一定会似懂连懂飞石雅到干李科的大门之外 ,皮尔等人的试验,和出端 枚硬币,出正的领率为:0.5181,0.5069. “洪湖水,液打准”很明是,在这一堆不瑞定的数的骨后,有一个确定的数操智 着它幻.这个数是0.5000一概率。 寻找不确定象背后的定因素,是这门学科的核心新究课题。 可裂商餐装子具精材时又多更华学”,多大反复质果更佳
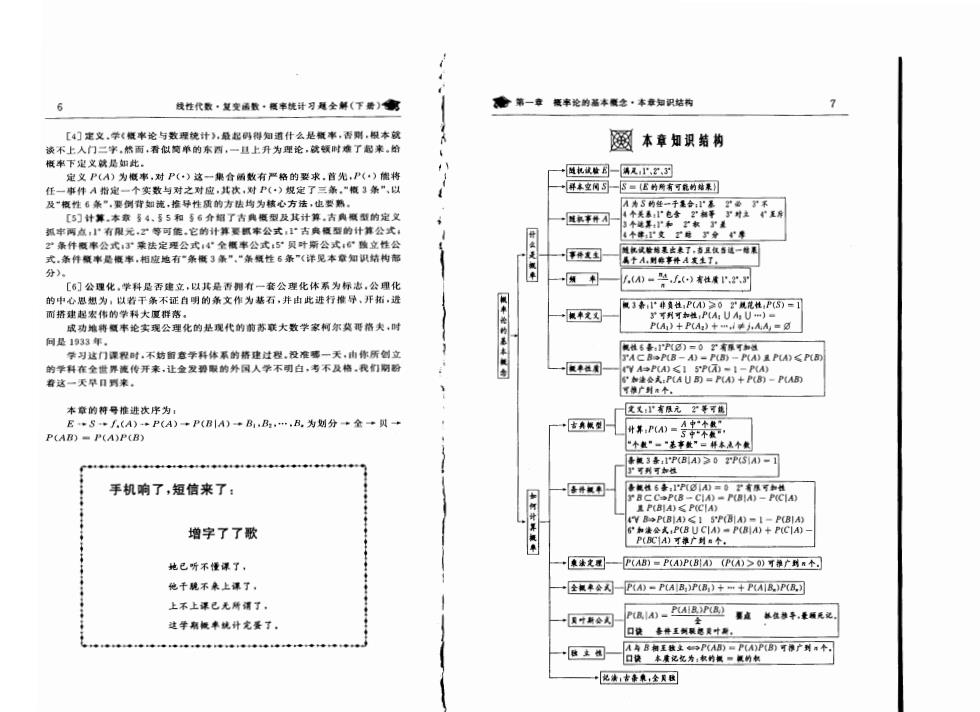
线性代数·复变函数·顺率统计习通全解(下黄)廊 第一立 率论的本顺·本知积姑构 2 [4]定义,学《概率论与数理统计),最起码得知道什么是概率,否则:根本就 谈不上人门二字,然面,看似简单的东西,一旦上升为理论,就顿时难了起来。给 圆本章如识结物 概率下定义就是如此 定义P(A)为概事,对P()这一集合函数有严格的要求,首先,P()将 任一事件A指定一个实数与对之对应,其次,对P(·)规定了三条,”恒3条”,以 本空一(E的所有可的结来】 及“授性6条“,要倒背如流,推导性质的方法均为核心方法,也要熟。 A为5的任一于是合:”系0了不 [5计算.本章多4,5和56介相了典顺型及其计算,吉型的定义 弧两点,”有限元,等可能,它的计算要公式1”古典 的计算公式 个准变于分?奉 艺条件微率公式:于乘法定理公式:4”全概率公式:5贝叶渐公式心做应性公 式条件顾率是概蜜,相应地有“条概3条“,“条疑性6条”(详见本章知识结构都 -事件发国 分) [6]公理化,学科是否建立,以其是香列有一套公理化体系为标志,公里化 ()-坠,.()有性情.”5 的中心思想为,以若干条不证自明的条文作为基石,并由此进行增导,开拓,近 而搭建起索伟的学科大厦群落。 规华定又 成功堆蒋率论实现公理化的是现代的前苏联大数学家柯尔莫延格,时 P(A)+P(A:)= 间是1933年 学习这门课程时,不妨留意学科体系韵精建过程,没准哪一天,由你所创立 的学科在全世界流传开来,让金发碧眼的外国人学不到白,考不及格.我们阴酚 便单性国 着这一天早口来。 本章的料号推进次序为: 文又护有限元公蒂可能 ESf,(A)P(A)+P(B|A)+B,B.B.为划分+金+贝+ 计养:PA)=中二个整, P(AB)-P(A)P(B) 3P(BA)≥02rP51A)-1 可列可 手机响了,短信来了: BCC-P(B -CIA)-P(BIA)-P(CIA) P(CIA 增字了了歌 P(BCA)可推广到a◆ 地已听不慢课了, 法克AB)=P(AP(B引)(PA)>0)可广m个 他干镜不上课了 全会PA-P(ABP(B)++PAR)P(司 上不上课已无所谓了, -因中新◆人因 )-PAB四事在k#手,泰插无之, 这学有版来统计宠餐了, 口快泰件互刻限愿风中数。 →PA)=P(A)PB)可广到个 之清专泰来,全天因

提性代数·复变函数·服率统计习题全解(下骨)廊 香第一章廉率论的基本凝念·习题全解 9 郎习题全解 (1)(A UB)C -(D:UDI U D.U D,U D:U D.) (D:U D:U D.U D)-D,U D:UD. AC U BC (D:U D)U (D:U D.) S1.1随机试验§1.2样本空间、随机事件 (2)AB UC-D,U D:UC D UC (AUC)(BUC)-(AUCnB)U(AUC 11* 写出下列随机试验的样本空何 ∩C)=DUD:UD,UC-DUC (1)记录一个小班一次数学考试的平均分数(设以百分制记分), 4.0指出下列命题中哪些成立,哪些不成立? (2)生产产品直到有10件正品为止,记朵生产产品的总件数。 (1)AUB=AEUB成立 (3)对某工厂出厂的产品进行检查,合格的记上“正品“,不合格的记上“次 (2)AB=AUB不戚立AB表示“事件A不发生而且B发生" 品”,如连续查出2个大品就停业检查,或检查4个产品就停止检查,记录检查的 AUB表示“A,B至少有一个发生”显然不等. 结果。 (4)在单位圆内任意取一点,记录它的坐标 (5)同时掷 (4)(AB)(AB)- 成立 三预设子,记录三模数子点数之和 (6)将一尺之捶折成三段,观泰各段长度, (5)若ACB,则A=AB, 成立 要点人们不能事先确定试验的哪一个结果一定发生,但可事先知道所 (6)若AB=⑦且CCA,则BC=②R立 有可能的结果,它们的集合即样本空间,往后计算率时,首先得知道S=? 《7)若ACB,则BC不 成立 (8)若BCA,则AUB-A 成立 解(1)S={一01,100n}其中#为小班人数 50设S={z0x≤2,A-{x号<x1,B-{zlr< (2)S一{x1x≥10,x为整数 (3S-{00.100,010,1100,1010,0110,1110,110,1011,0111,1111,0表 是1,具体写出下列各事件1)万B(2不UB(3)万0西 示次品】表示正品。 (40={(xy)x2+y<1:(5)5=(3,4.,18) 解A=5-A=(红0云x云之或1<x发2》 (6)设xy,分别表示三段长度,则5-【x,y,)x之0y>00 x+y+=1 1B-川片≤≤含或1<r<是) 2中2设A,B,C为三事件,用A,B,C的运算关系表示下列各事件。 (2)AUB-{x10≤x≤25 (1)A发生,B与C不发生,(2)A与B都发生,而C不发生 (3)A西=万U万=AUB=z}云x<是 (3)A,B,C中至少有一个发生:(4)A.B,C都发生 (5)A,B,C都不发生,(6)A,B,C中不多于 个发生 (4)A百=S-AB{x0x≤号或1<x2 (7)A,B,C中 不多于两个发生(8)A,B,C中至少有两个发生 要点 试验结果出来丁,要看A是否发生,得看这个结果是香为A中一个 51.3频率与概率§1.4等可能概型(古典概型 元赏,须认真体会“事件发生“这一重要就念,否则,本课程无法入门! 解(1)AEC(2)ABC (3)A U B UC ()ABC (5)A8C 6.3设A,B为两事件且P(A)-0.6,P(B)=0.7,问(1)在什么条件 Ds/DD. 下P(AB)取到最大值,最大值是多少?(2)在什么条件下P(AB)取到最小值, (B)AB U BC U AC 最小值是多少? 3◆0用作图的方法说明下列各等式 要点思考将P(A),P(B),P(AB)联系在一起的公式 (1(A UB)C AC U BC. P(A UB)=P(A)P(B)-P(AB) (2)AB UC-(A UC)(B UC) 解(1)观察上式,已知P(A),P(B)均固定,当P(AUB)最小时,P(AB) 如图11. 图1 最大,当AUB=B,即ACB时,P(AUB)最小,此时P(AB)取到最大值: 最大为P(AB)=P(A)=0.6: (2)当P(AUB)最大时,P(AB)最小.当AUB-S时,P(AUB)取得 ·题号编持衣序,二服中三版,数字0表示没有此愿。 最大值为1,此时,P(AB)取得最小值,最小值为P(AB)=P(A)十P(B)

10 线性代数·复变函数·概率使计习题全解(下椅)雪 意第一章概率论的基本餐在·习题全解 11 P(AUB)=0.6+0.7w1=03. 74设A,B,C为三事件,且P(A)-P(B)=P(C)=},P(AB) 准,2精红镶的种数为C,C,6好州所求概率为S~:G-器 P(BC)=0.P(AC)=号,求A,B.C至少有一个发生的额半. 12°8在1500个产品中有400个次品,1100个正品,任取200个.(1)求 恰有90个次品的概事,(2)求至少有2个次品的概率。 要点用字母表示率件,是本课程入门的又一关健。由“至少”联想“U”, 要点 基本事件:从1500个产岛中任进200个,组合同题:由“至少”联想 遵而想到公式: P(A)=1-P(A P(A UB UC)-P(A)+P(B)P(C)-P(AB)-P(BC)- 解 S中个数C P(AC)+PCARC) (1)有90个次品的选法种数C。·C,所求概率为C·C/C: 解至少有一个发生,A【1B1 P(AU BUC)- P(A)+P(B)+P(C)-P(AB)- (2)没有次品的概率P0一C/C。 P(BC)-P(AC)+P(ABC) 有一件次品的概率p:一C·C8/C8 至少有两件次品的概率 -分+分+寻-0-0-音+0-吾 p-1-p一p-1-C0/Cw。一C1·C8/C8o 其中 P(ABC)≤P(AB)=O→P(ABC)-O 13⊙9从5双不同的鞋子中任取4只,这4只鞋子中至少有两只鞋子配成 85在一标雅英语词典中有55个由两个不相同的字母所组成的单词, 一双的每率是老少 解法1 样本点总数为P。,记A一“4只鞋子中至少有2只是一双”,则对 立事件A=“4只鞋子均不成双”,故第一只鞋子是从5双(10只)中任取一只 要点题8⊙5一题1612为古典概型所对应习题,PA)=分千,分子 有10种取法,第二只鞋子从剩下的4双(8只)中任取一只,有8种败法,第三只 一A中基本事件个数,分母一S中基本事件个数,首先要弄清燕本事件是什么, 鞋子从再剩下的3双(6只)中任取一只,有6种取法,第四只鞋子有4种数法,故 再用排列组合知识计算网 事件A所包含的样本点总数为10×8×6×4,得 “数” 基本事件,从26中选1,再从(26一1)中选1.S中个数-P,则能排 Pa=1-Pa)-1-18x8x8x9- 上述单词的概率P一亮一品 解法2A中个数是从5双不同鞋子中任取4双,再从每双中任报一只的不 ⊙0 在屯话号码薄中任取一个电话号码,求后面四个数全不相同的概率 同取法的种数,共有C×2种取法,故 (设后 四个数中的每一个数都是等可能地取0,1.,9)。 PA)=1-P(a=1-C×2/C- 解所有可能的种数为10×10×10×10种,后四个数全不相同的种数 解法3记A1=“取出的4只鞋子中恰有2只配成一双”,A?=“散出的4 为P则所求缀率为总-器 只鞋子 好配成 -4:UA: A=0 10.6在房间里有10个人,分别佩戴从1号到10号的妃意章,任选3个 A,中个数为从5双鞋子中任取一双,再从另外4双中取不能配对的两只 记录其纪念章的号码 共有CG-C种取法数从看PA)=CCC尘-异 C。 (1)求最小 号码为 5的率:(2)求最大号码为5的摄率, A:中个数为从5双鞋子中任取2双的取法数,即有C子种取法,从面 样本空问S的样本点总数为C。, (1)最小号码为5是必须取到5号,而其余2人从6~10号中任取,故事件 P(A)=C好/Ci=2 的样本点个数为C,所求城率为=C/C。一立 所以 P(A)=P(A)十P(A=超 (2)最大号码为5,其余2人在14中选号,事件的样本点个数为C,所求 1410 在11张卡片上分别写上probability这11个字母,从中任意连抽 概率为p:=C/Ca一 7张,求其排列结果为ability的概率. 11.7某油公司发出17桶袖,其中白 解抽法总数为P,则抽到ability的疑率为 在搬运过程中所有标签脱落 0桶惑《桶,红3桶, ,交货人随意将这些袖漆发给顺客,问一个定货4 p=Lx2×2X1X1X1X1=0.00024 P 桶白漆,3桶照藤和2桶红,的鼷客能按所定领色如数得到货的概率是多少, 其中字母b有两种选择,第 一个字母i有两种择 要点从17桶中,选9(-4+3+2)桶,组合问题。 解设已给这些袖漆桶编号,则总的选法种数为C:,有4栖白漆,3桶网 15°11将3个球随机地故人4个杯子中去,求杯子中球的最大个数分别 为1,2,3的概*

12 线性代数·复变晒数·板率统计习题全解(下斯) 香第一章授率论的基本念·习题全解 13 要点球选杯子,面不是杯子选球。 解设3个球已有编号,球最大个数为1的种数为P:,球最大个数为2的 所求概率 种数为CC!C球最大个数为3的种数为C,所以球最大个数为123的 基本事件:掷两顺骰子,观察其点数 率分别为: S中个数=6X6一36 C·C·C A=11,6),(2.5),(3,4),(6,1).(5.2),(4,3)1,A中个数-6 P+CCC+C'P丹+GC·C+'P+C·CC+ AB={(1.6),(61)},AB中个数=2 P1)-吉 P(A) 16⊙1250只钉随机地取来用在10个部件上,其中有3个钉强度太 解法2将解法1中的A看做样本空同。 弱,每个部件用3只锦钉:若将3只强度太到的卿钉都装在一个部件上,则这个 P(B1A)-串餐-各-吉 中个数 部件强度校太羽。问发生一个部件强度太期的概率是多少? 解基本事件一“50个钉中任取3个”,S中基木事件个数=C= 20.16据以往资料表明,某一3口之擦,患某种传染病的概率有以下规 19600,令A“一个部件强度太”则A=“先从10个都件中选一个,再把三 排:P(孩子得病}=0.8,P{母亲得病|孩子得病)一0,5,P(父莱得病|母亲及 个期铆灯装在其上”,A中基本事件个数=CC3,则 孩子得树》一0.4,求母亲及孩子得病但父亲未得病的凝率 PA-e-g8-10 解设A=“孩子得病”,B=“母亲得病”,C■“父亲得病”,则所求概率 为P(ABC).已知P(A)-0,6,P(B|A)=0.5,P(C1AB)-0.4,则由乘法定 理有 P(AB)P(BIA)P(A)-0.3 §1.5条件概率§1.6独立性 P(ABC)P(CAB)P(AB)-0.12 AB-ABC U ABC.(ABC)(ABC)P(AB)-P(ABC)+P(ABC) P(ABC)=P(AB)-P(AB)=0.3-0.12■0.18 17⊙13已知P(A)=0.3.P(B)-0.4,P(AB)0.5,求P(B1AU 21.17已知在10只品体管中有2只次品,在其中取两次,每次任取一只, B). 作不放回抽样,求下列事件的概有, 要点用条件概率的公式将P(B引AUB)写开,然后,缺什么,补什么。 (1)两只都是正品:(2)两只都是次品(3)一只是正品,一只是次品(4)第 二次取出的是次品, 解法1设A一“2正",B=“2次”,C=“1正1次”,D=“第2次次”,基 由P(A)=0,3,P(B)=0.4,有P(A)-1-P()-0.7,P(B)-1 本事件一“取一只,不放回,再取一只”,S中个数=C,可利用古典凝型公式计 P(B)=0.6.由A=ABUAB,且(AB)(AE)-可,知P(A)=P(AB UAB) =P(AB)+P(AE,于是 算: PA)一串不 P(AB)=P(A)-P(AB)=0.7-0.5-0.2 DA中个数=G:于是PA)-是-碧 将具体数代人后有:P(B1MUB)一a7+8后-05=专=0.25 1814已知P(A)-,P(BA)=,P(A1B)=之,求P(AUB). ②)B中个数=,于是P()=是= 解P(A)=子>0,由乘法定理有:P(AB)-PA),P(B1A)-立 ac中个数-cG,手是P0)-器-碧 又由PAB)-PAB)P(B)有:P(B)=器=号=音 (4)D一“第一次取出正且第二次取出次”U“第一次取出次且第二次取出 P(A U B)P(A)+P(B)-P(AB)=+= D中个数-9+9,于是P(D)=CG/2+GG2=专 2 1915掷两顺骰子,已知两颗觳子点数之和为7,求其中有一期为1点的 概率(用两种方法), 解法2设事件如解法1,又设A1一“第1次正”A:=“第2次正”.则瓦 要点解法1,考泡整个样本空向,解法2,将已发生的事件当做样本空间, =“第1次次”,A:=“第2次次”,用舜法公式算 解法1设A=“两颗般子点数之和为?“,B=“有一颗子点数为1”,则 (IP(A)-P(AA)-P(A)P(AIA)-是×号=-器