
第三节条件分布 一、离散型随机变量的条件分布 二、连续型随机变量的条件分布
一、离散型随机变量的条件分布 二、连续型随机变量的条件分布 第三节 条件分布

一、离散型随机变量的条件分布一一条件分布律 定义设(X,Y)是二维离散型随机变量,分布律为 P{X=x,Y=yj}=Pu,i,j=1,2,., 对于固定的j,若PY=y}>0,则 X)P(XD(1.2) P(Y=y} P.j 称为在Y=y,条件下X的条件分布律。 对于固定的i,若P{X=x,}>0,则 PIY=Y X-x)-AX-XY-y P{X=,} 2(j=1,2, P 称为在X=x,条件下Y的条件分布律
称为在Y y = j条件下 X 的条件分布律。 { } P X x Y y = = i j ( 1,2, ) i = { , } { } i j j P X x Y y P Y y = = = = ij j p p• = 一、离散型随机变量的条件分布 对于固定的 j,若 { } 0 P Y y = j ,则 定 义 设 (X,Y)是二维离散型随机变量,分布律为 { , } , , 1,2, P X x Y y p i j = = = = i j ij , ——条件分布律 { } P Y y X x = = j i ( 1,2, ) j = { , } { } i j i P X x Y y P X x = = = = ij i p p • = 对于固定的 i,若 { } 0 P X x = i ,则 称为在 X x Y = i 条件下 的条件分布律

Px==,= (i=1,2,) 即 P.i P(Y=yX=x)=Pu (j=1,2,) 注:作为条件的随机变量的取值是固定的。 条件概率的性质:10PX=xY=y≥0: 2°∑P{X=x,lY=y}=1 i- 例1在一汽车工厂中,一辆汽车有两道工序是由机器人 完成的。其一是紧固三只螺栓,其二是焊接2处焊点。以X 表示机器人紧固的螺栓坚固得不良的数目,以Y表示由机器 人焊接的不良焊点的数目。据积累的资料知(X,Y)的分布 律如下:
{ } P X x Y y = = i j ( 1,2, ) i = ij j p p• = { } P Y y X x = = j i ( 1,2, ) j = ij i p p • = 即 例 1 在一汽车工厂中,一辆汽车有两道工序是由机器人 完成的。其一是紧固三只螺栓,其二是焊接 2 处焊点。以 X 表示机器人紧固的螺栓坚固得不良的数目,以 Y 表示由机器 人焊接的不良焊点的数目。据积累的资料知(X,Y)的分布 律如下: 条件概率的性质: 1 0 P{ X= xi |Y= yj }0; 0 1 2 { | } 1 i j i P X x Y y = = = = 注:作为条件的随机变量的取值是固定的
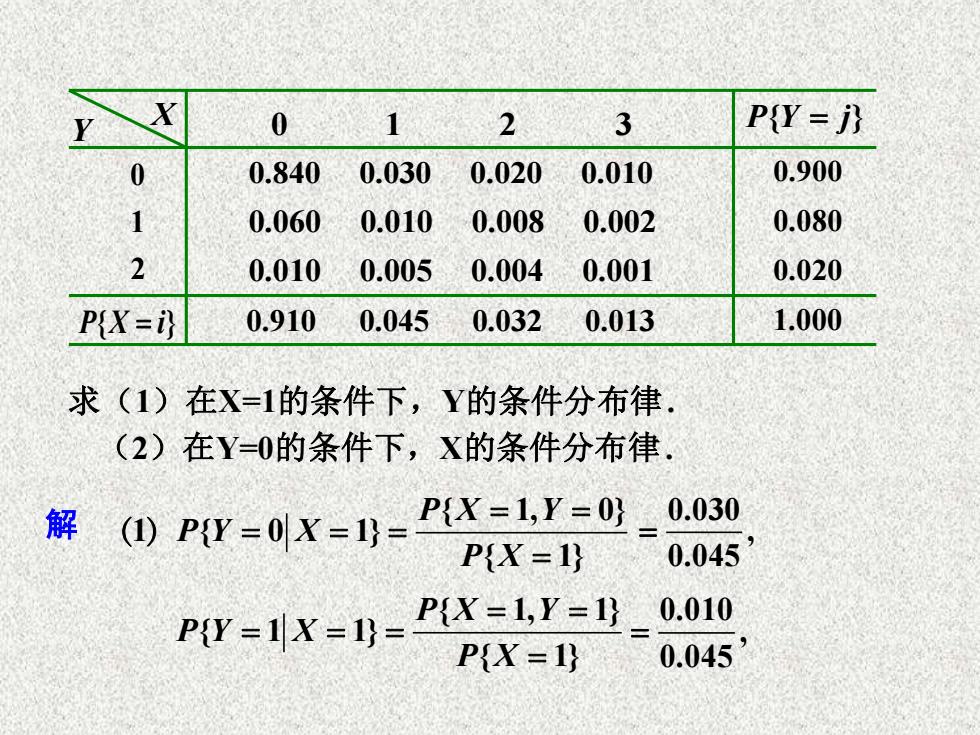
0 1 2 3 P(Y=j) 0 0.840 0.030 0.020 0.010 0.900 1 0.060 0.010 0.008 0.002 0.080 2 0.010 0.005 0.004 0.001 0.020 P(X=i 0.910 0.045 0.0320.013 1.000 求(1)在X=1的条件下,Y的条件分布律. (2)在Y=0的条件下,X的条件分布律. 解 ①PW=0x=1=PX=1,y=0 }0.030 P{X=1} 0.045 POY=1X=1)-P(X=LY=B 0.010 PX=1} 0.045
X Y 0 1 2 3 0.840 0.030 0.020 0.010 0.060 0.010 0.008 0.002 0.010 0.005 0.004 0.001 0 1 2 0.900 0.080 0.020 P X i { } = 0.910 0.045 0.032 0.013 1.000 P Y j { } = 解 求(1)在X=1的条件下,Y的条件分布律. (2)在Y=0的条件下,X的条件分布律. { 1, 0} 1 { 0 1} { 1} P X Y P Y X P X = = = = = = ( ) 0.030 , 0.045 = { 1, 1} { 1 1} { 1} P X Y P Y X P X = = = = = = 0.010 , 0.045 =

PY=2X=1}=PX=1,y=20.005 P{X=1} 0.045 即在X=1的条件下,Y的条件分布律为 Y=k 01 2 P(Y=kX=1) (2)同理可得,在Y=0的条件下,X的条件分布律. X=k 0 1 23 P(X=kY=0) 84321 9090 90 90
Y k = P Y k X { 1} = = 0 1 2 6 2 1 999 即在 X Y = 1 , 的条件下 的条件分布律为 (2)同理可得,在Y=0的条件下,X的条件分布律 . X k = P X k Y { 0} = = 0 1 2 3 84 3 2 1 90 90 90 90 { 1, 2} { 2 1} { 1} P X Y P Y X P X = = = = = = 0.005 , 0.045 =