
由高阶导数公式,上式又可写成 e-空贤e-r+a 1=0 英风a-2知三ge-r5 若lim Ry(z)=0, N->oo 可知在内@/-y n!
由高阶导数公式, 上式又可写成 − = = − + 1 0 0 0 ( ) ( ) ( ) ! ( ) ( ) N n N n n z z R z n f z f z 其中 − − = = + K n N n N n z z z f i R z ( ) d ( ) ( ) 2π 1 ( ) 1 0 0 lim ( ) = 0, → R z N N 若 可知在K内 = = − 0 0 0 ( ) ( ) ! ( ) ( ) n n n z z n f z f z 6
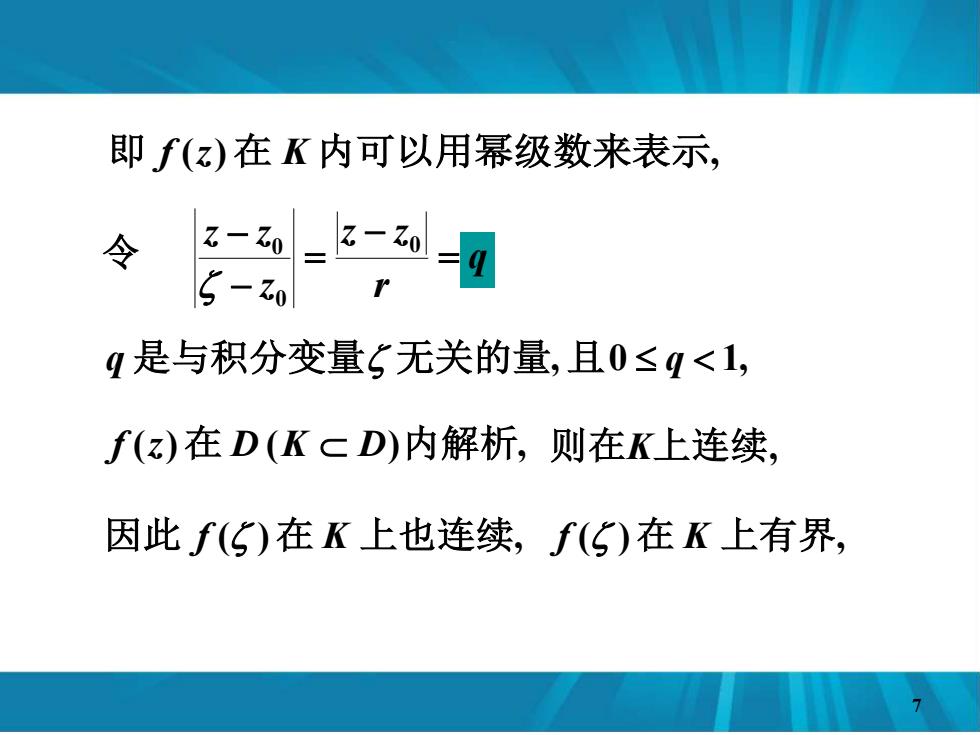
即f(z)在K内可以用幂级数来表示, 令 - 0=z- 5- 0=q q是与积分变量5无关的量,且0≤q<1, f(z)在D(KcD)内解析,则在K上连续, 因此f(5)在K上也连续,f(5)在K上有界
即 f (z)在 K 内可以用幂级数来表示, 令 q r z z z z z = − = − − 0 0 0 f (z)在 D (K D)内解析, 则在K上连续, q 是与积分变量 无关的量, 且0 q 1, 因此 f ( )在 K 上也连续, f ( )在 K 上有界, 7

即存在一个正常数M,在K上f(5)≤M. R,age-u n s,1.M 2r=9 2πr 21-q
即存在一个正常数M, 在K上 f ( ) M. z z s z f R z K n N n N n ( ) d ( ) ( ) 2π 1 ( ) 1 0 0 = + − − − − − K n=N n s z z z z f d ( ) 2π 1 0 0 0 = n N n q r r M 2 2 1 . 1 q Mq N − = 8

Iimq”=0→lim Ry(z)=0在K内成立, N->oo N> 从而在K内 泰勒级数 n=0 n! f(z)在z的泰勒展开式, 说明: (1)从证明可知,函数f(z)在z处的幂级数的收敛 半径至少等于从z到D的边界上点的最短距离
lim = 0 → n N q lim ( ) = 0 K → R z N N 在 内成立, 从而在K内 = = − 0 0 0 ( ) ( ) ! ( ) ( ) n n n z z n f z f z f (z) 在 z0 的泰勒展开式, 泰勒级数 9 说明: . (1) , ( ) 0 0 半径至少等于从 到 的边界上点的最短距离 从证明可知 函数 在 处的幂级数的收敛 z D f z z

(2)如果函数f(z)在D内有奇点a,则使f(z)在z的 泰勒展开式成立的R,等于从z到f(z)的距z最近 的一个奇点a之间的距离,即R=a-o (3)函数f(z)在z处的泰勒展开式是惟一的 设f(z)在。已被展开成幂级数: f(2)=a+a(z-2o)+a2(z-2)2+. +an(2-2o)”+., 10
, . , ( ) (2) ( ) , ( ) 0 0 0 0 a R a z R z f z z f z D a f z z 的一个奇点 之间的距离 即 = − 泰勒展开式成立的 等于从 到 的距 最近 如果函数 在 内有奇点 则使 在 的 (3) ( ) . 函数f z 在z0 处的泰勒展开式是惟一的 10 ( ) : 设 f z 在 z0 已被展开成幂级数 f (z) = a0 + a1 (z − z0 ) + a2 (z − z0 ) 2 + ( ) , + an z − z0 n +