
注①定理的条件:分子分母都是无穷小;分子分母都可导,且分母的导数不等于0;导数之比的极限存在或为80②定理的结论:函数之比的极限等于导数之比的极限f'(x)若lim还是未定式,且f'(x),F"(x)满足F'(x)x-a定理中对f(x),F(x)所要求的条件,则可继续使用法则,直到不再是未定式为止f"(x)= lim?limx-a F"(x)F(x)x→a
注 ①定理的条件:分子分母都是无穷小;分子分母 都可导,且分母的导数不等于0;导数之比的 极限存在或为∞ ②定理的结论:函数之比的极限等于导数之比的 极限 ③ ( ) lim ( ), ( ) ( ) ( ), ( ) x a f x f x F x F x f x F x → 若 还是未定式,且 满足 定理中对 所要求的条件,则可继续 使用法则,直到不再是未定式为止 ( ) ( ) lim lim ( ) ( ) x a x a f x f x → → F x F x = ( ) lim ( ) x a f x → F x = =

将x→a换成x→at,x→a ,x→+80,x→-0,0x→oo的型及-型未定式都有类似的结论:08如:x→8时型的极限0定理22设(1)当x→o时,函数 f(x)及F(x)都趋于零;(2)当Ix>N时,f(x)及 F'(x)都存在,且 F'(x)0;f'(x).存在(或为无穷大);(3) limF'(x)x-→0f(x)-那末limF(x)X→8
④ , , , , 0 0 x a x a x a x x x → → → → + → − + − → 将 换成 的 型及 型未定式都有类似的结论: 时 型的极限 0 0 如: x → 定理2 (1) , ( ) ( ) ; (2) | | ( ) ( ) ( ) 0; ( ) (3) lim ( ); ( ) ( ) ( ) lim lim . ( ) ( ) x x x x f x F x x N f x F x F x f x F x f x f x F x F x 设 当 时 函数 及 都趋于零 当 时, 及 都存在,且 存在 或为无穷大 那末 → → → → =

cosxU例1 求lim()元元x2x2(cos x)sinx解 原式=limlim=-1.1T元元C-x→X222x3 - 3x+2例2求 lim1x-x2-x+10x-13x2-336x解原式=limlimx-13x2-2x -12x-16x - 2
例 1 例 2 解 . 1 3 2 lim 3 2 3 1 − − + − → x x x x x x 求 3 2 1 3 3 lim 2 2 1 − − − = → x x x x 原式 6 2 6 lim1 − = → x x x . 23 = ) 00( ) 00( 解 2 cos lim . 2 x x x 求 2 (cos ) lim ( ) 2 x x x 原式 → = − 2 sin limx 1 x → − = 1
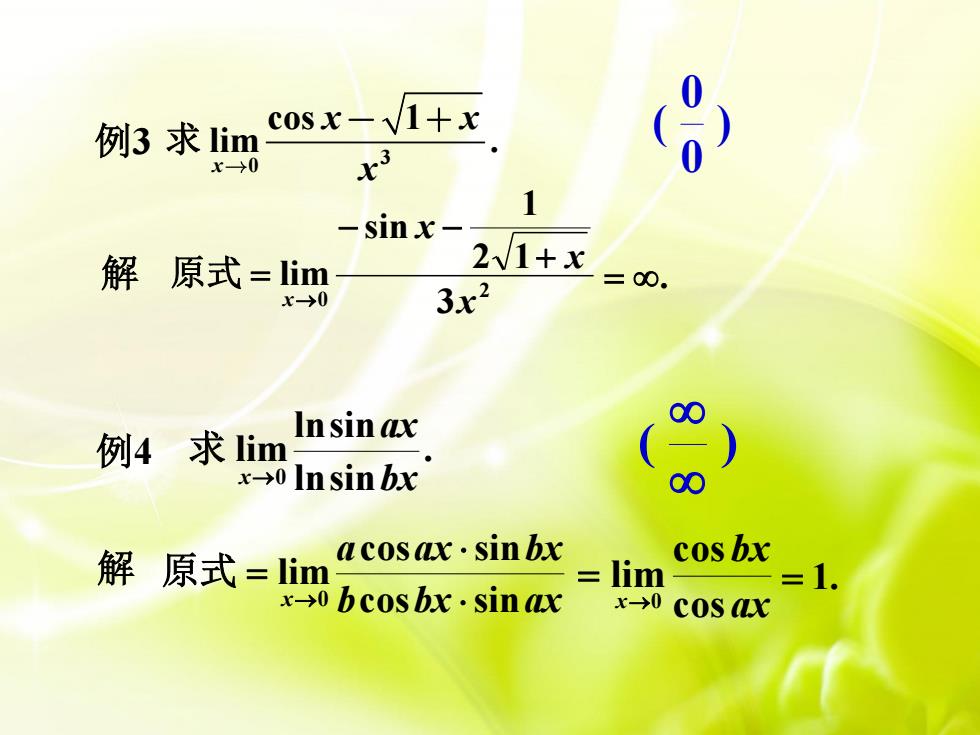
/1+xcosx-例3求lim0ox→01-sinx2/1+x解原式=lim=8.3x2x-08In sin ax求 lim例4x-→>0 In sin bx8acosax·sinbxcosbx解原式=limlim1x-o bcosbx.sinaxx-→0cosax
例 3 例 4 解 . lnsin lnsin lim0 bx ax x→ 求 b bx ax a ax bx x cos sin cos sin lim0 = → 原式 = 1. ) 00(( ) ax bx x cos cos lim→0 = 3 0 cos 1 lim . x x x x 求 2 0 3 2 11 sin lim x x x x + − − = → 解 原式 =

8Inx例5 (1)求lim(n>0).th8X→+11xlim:0原式= lim二解hrr-1x-→+80x-→+8nxth(2)求 lim(a>0)erx-→+00nxh-1n!解:原式= limlima"eix =0.AeixX-→+00x-→+0由此可以看出三类函数的增大速度eix >x" >ln x (x →+o0)
例 5 解 ln (1) lim ( 0). n x x n →+ x 求 1 1 lim n x x nx →+ − 原式 = 1 lim 0 n x→+ nx = = (2) lim ( 0) nx x xe →+ 求 1 lim n x x nxe − →+ 解:原式 = ! lim n x x ne →+ = = = 0. ( ) ln ( ). x n e x x x → + 由此可以看出三类函数的增大速度