
第二节微积分基本公式问题的提出二、积分上限函数及其导数三、牛顿一菜布尼茨公式四、小结
第二节 微积分基本公式 • 一、问题的提出 • 二、积分上限函数及其导数 • 三、牛顿—莱布尼茨公式 • 四、小结

问题的提出一变速直线运动中位置函数与速度函数的关系设某物体作直线运动,已知速度v=v(t)是[T,T,]上的一个连续函数,且(t)≥0,s=s(t)是位置函数,求物体在这段时间内所经过的路程(v(t)dt变速直线运动中路程为另一方面这段路程可表示为 s(T)-s(T)v(t)dt = s(T)-s(T). 其中 s(t)=v(t).一般的,设f(x)在[a,b]连续,且F'(x)=f(x)' f(x)d?F(b) - F(a)
变速直线运动中位置函数与速度函数的关系 变速直线运动中路程为 2 1 ( ) T T v t dt 另一方面这段路程可表示为 ( ) ( ) 2 T1 s T − s F x f x ( ) ( ). = ( ) ( ) ( ). 2 1 2 1 v t dt s T s T T T = − 其中 s(t) = v(t). 一般的,设f(x)在[a,b]连续,且 ( ) ( ) ( ). b a f x dx F b F a = − 一、问题的提出 1 2 ( ) [ , ] ( ) 0 ( ) v v t T T t v t s s t = = 设某物体作直线运动,已知速度 是 上 的一个连续函数,且 , 是位置函 数,求物体在这段时间内所经过的路程

二、积分上限函数及其导数设函数f(x)在区间[a,b|上连续,并且设x为[a,b|上的一点,在区间[a,x]考察定积分f f(x)dx= f" f(t)dt如果上限x在区间[a,b上任意变动,则对于每一个取定的x值,定积分有一个对应值,所以它在[a,b定义了一个函数记@(x)= f, f(t)dt.积分上限函数
x a f (x)dx = x a f (t)dt ( ) ( ) . x a x f t dt = 记 积分上限函数 二、积分上限函数及其导数 ( ) [ , ] [ , ] [ , ] f x a b x a b a x 设函数 在区间 上连续,并且设 为 上的一点,在区间 考察定积分 [ , ] [ , ] x a b x a b 如果上限 在区间 上任意变动,则 对于每一个取定的 值,定积分有一个对 应值,所以它在 定义了一个函数
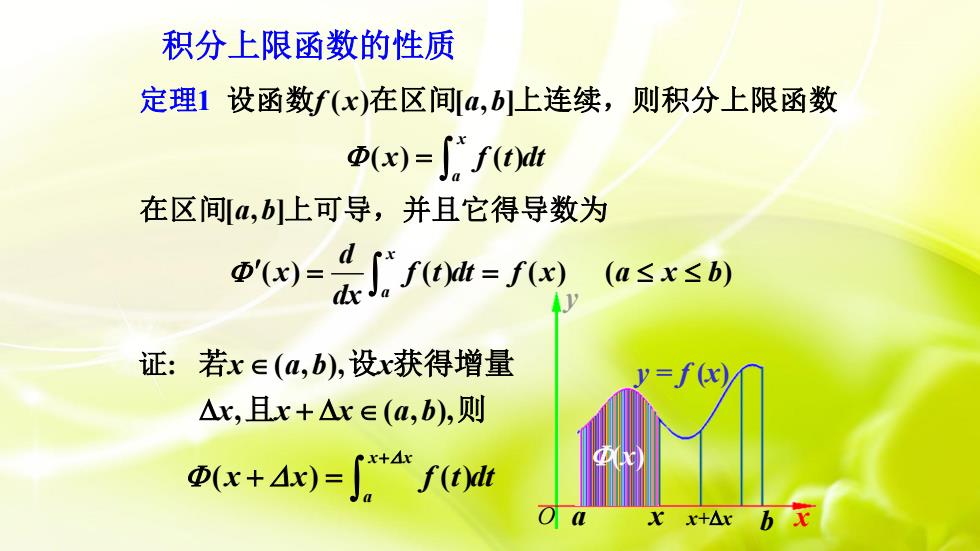
积分上限函数的性质定理1设函数f(x)在区间[a,b]上连续,则积分上限函数d(x) = , f(t)dt在区间[a,b上可导,并且它得导数为d@'(x) =[ f(t)dt = f(x)(a≤x≤b)dr.证:若xE(a,b),设x获得增量Ax,且x+Ar(a,b),则D(x + 4x) = J++ f(t)dtxoaxbx+Ar
积分上限函数的性质 证: ( ) ( ) x x a x x f t dt + + = ( , ), , ( , ), x a b x x x x a b + 若 设 获得增量 且 则 ( ) [ , ] ( ) ( ) [ , ] ( ) ( ) ( ) ) 1 ( x a x a f x a b x f t dt a b d x f t dt f x a x b dx = = = 设函数 在区间 上连续,则积分上限函数 在区间 上可导,并且它 为 定 得导数 理 a x x+x b x y y = f (x) (x) O
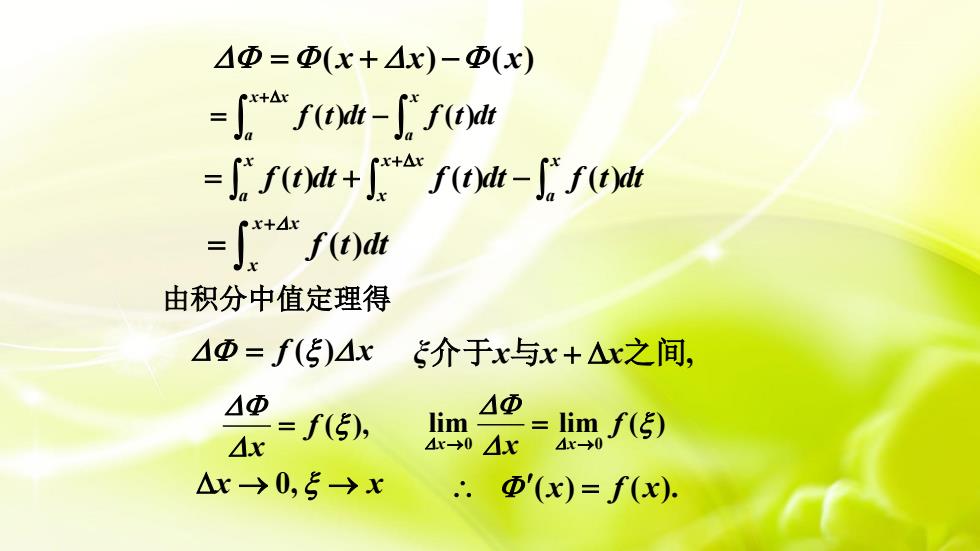
4@ = @Φ(x + 4x)-@(x)- f*+ f(t)dt -f' f(t)dt= J" f(t)dt + *+" f(t)dt - f" f(t)dtx+4xf*+" f(t)dt由积分中值定理得4@ = f()4x介于x与x+Ax之间4@4@limlim f()=f(5),4xAx4x-→04x-0Ax→0,5→x:: @(x)= f(x)
f t dt f t dt f t dt x a x x x x a = + − + ( ) ( ) ( ) ( ) x x x f t dt + = 由积分中值定理得 = f x ( ) ξ介于x x x 与 + 之间, x → 0, → x f ( ), x = 0 0 lim lim ( ) x x f x → → = = ( ) ( ). x f x = + − ( ) ( ) x x x f t dt f t dt x a x x a = − + ( ) ( )