
第四节反常积分一、无穷限的反常积分二、无界函数的反常积分·三、小结
第四节 反常积分 • 一、无穷限的反常积分 • 二、无界函数的反常积分 • 三、小结

无穷限的反常积分定义1 设函数f(x)在区间[a,+)上连续,取b>a如果极限 lim「"f(x)dx存在,则称此极限为函数f(x)在区间[a,+o0)上的反常积分,记作[f(x)dx" f(x)dx = lim [" f(x)dx当极限存在时,称反常积分收敛:当极限不存在时,称反常积分发散
一、无穷限的反常积分 1 ( ) [ , ) lim ( ) ( ) [ , ) ( ) ( ) lim ( ) . b b a a b a a b f x a b a f x dx f x a f x dx f x dx f x dx →+ + + →+ + + = 定义 设函数 在区间 上连续,取 如果极限 存在,则称此极限为函数 在区间 上的 记作 当极 反常积分, 限存在时,称反常积分收敛;当极限不存在 时,称反常积分发散

类似的,设函数f(x)在区间(-80,b上连续,取a<b如果极限lim「"(x)dx存在,则称此极限为函数f(x)在区间(-o,b)上的反常积分,记作[ f(x)dx", f(x)dx= lim f' f(x)dx当极限存在时,称反常积分收敛:当极限不存在时,称反常积分发散
( ) ( , ] lim ( ) ( ) ( , ] ( ) ( ) lim ( ) . b a a b b b a a f x b a b f x dx f x b f x dx f x dx f x dx →− − − →− − − = 类似的,设函数 在区间 上连续,取 如果极限 存在,则称此极限为函 数 在区间 上的反常积分,记 反常积分收敛 作 当极限存在时,称 ;当极限不 反常积 存 时,称 分发散 在

设函数f(x)在区间(-0,+)上连续,如果反常积分[~ f(x)dx和J f(x)dx都收敛,则称上述两反常积分之和为函数f(x)在无穷区间(-80,+80)上的反常积分,记作:J f(x)dx- f(x)dx = J (x)dx+ Jt° f(x)dx= lim (" f(x)dx+ lim [' f(x)dxh+oa极限存在则称反常积分收敛:否则,称反常积分发散
0 0 0 0 ( ) ( ) ( ) lim ( ) lim ( ) b a b a f x dx f x dx f x dx f x dx f x dx + + − − →− →+ = + = + 0 0 ( ) ( , ) ( ) ( ) ( ) ( , ) ( ) f x f x dx f x dx f x f x dx + − + − − + − + 设函数 在区间 上连续,如果反常 积分 和 都收敛 反常积分, ,则称上述 两反常积分之和为函数 在无穷区间 上的 记作: 极限存在则称反常积分收敛;否则,称反常积分发散
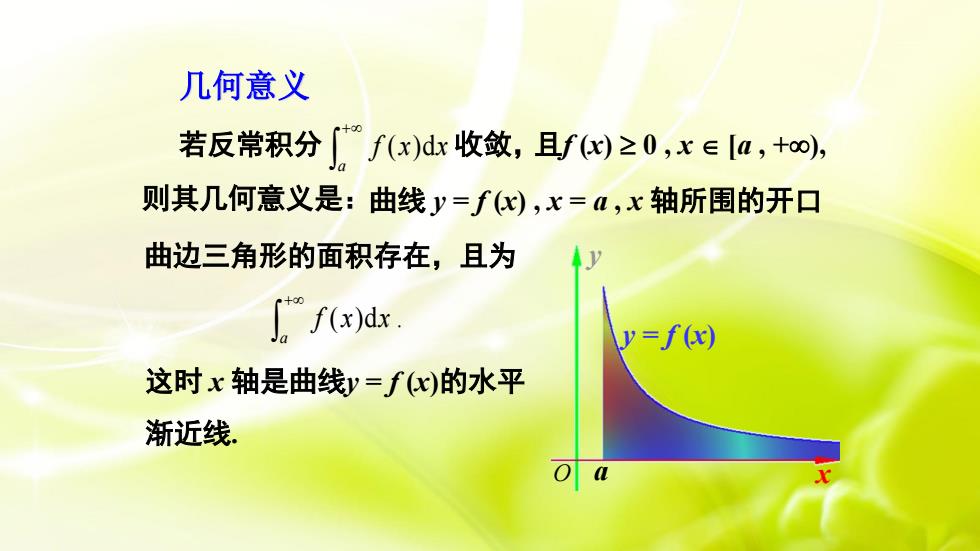
几何意义若反常积分f(x)dx收敛,且f(x)≥ 0 ,x E [a,+o0),则其几何意义是:曲线y=f(x),x=a,x轴所围的开口曲边三角形的面积存在,且为ft* f(x)dx.y=f (网)这时x轴是曲线y=f(α)的水平渐近线Oa
几何意义 若反常积分 + a f (x)dx 收敛, 则其几何意义是: 曲边三角形的面积存在,且为 ( )d . + a f x x 这时 x 轴是曲线y = f (x)的水平 渐近线. 且f (x) 0 , x [a , +), 曲线 y = f (x) , x = a , x 轴所围的开口 a x y y = f (x) O