
第七节常系数齐次线性微分方程、二阶情形下的定义解法和举例n阶情形下的定义解法和举例
第七节 常系数齐次线性微分方程 一、二阶情形下的定义解法和举例

第六章定积分的应用一、二阶常系数线性齐次微分方程形如EO(是常数)定义的方程称为二阶常系数齐次线性微分方程,如果p,q不全是常数,则称之为二阶变系数齐次线性微分方程y"+ 2y'-5y = 0,例如:二阶常系数齐次线性微分方程y"+2y+3xy=0.二阶变系数齐次线性微分方程■第一节定积分的元素法
第一节 定积分的元素法 第六章 定积分的应用 一、二阶常系数线性齐次微分方程 二阶常系数齐次线性微分方程 二阶变系数齐次线性微分方程 定义 ᵯ ″ + ᵯ 形如 ′ + ᵯᵯ= 0 (ᵯ,是常数) 例如: y ″ + 2y ′ − 5y = 0, y ″ + 2y ′ + 3xy = 0

第六章定积分的应用2.解法由二阶齐次线性微分方程通解的结构可知,要求通解就是要求它的两个线性无关的特解,那么如何求两个线性无关的特解呢?函数与其一阶、二阶导数只差一个常数因子为此先来分析方程的特点:y"+py+qy=O(pg是常数)而指数函数y=erx(r为常数)刚好具有这一特性因此可用指数函数e为常数)来尝试■第一节定积分的元素法
第一节 定积分的元素法 第六章 定积分的应用 就是要求它的两个线性无关的特解. 那么如何求两个 线性无关的特解呢? 为此先来分析方程的特点: 函数与其一阶、二阶导 数只差一个常数因子. 2. 解法 由二阶齐次线性微分方程通解的结构可知, 要求通解 y ″ + py ′ + qy = 0(p,q是常数) 因此可用指数函数ᵯ= eᵯᵯ(r为常数)来尝试
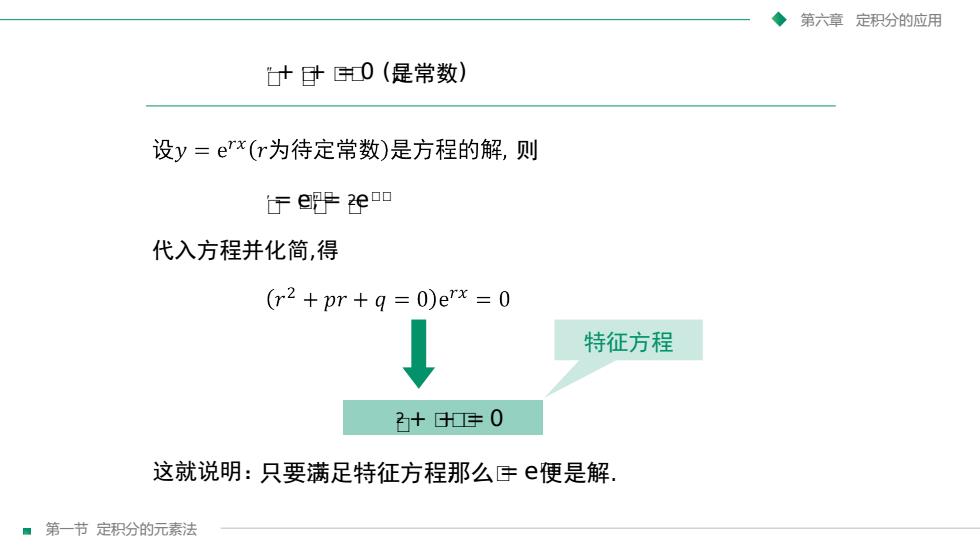
第六章定积分的应用 (是常数)设y=erx(r为待定常数)是方程的解,则FeF2e0代入方程并化简,得(r2 +pr + g = 0)erx = 0特征方程2+E0这就说明:只要满足特征方程那么e便是解■第一节定积分的元素法
第一节 定积分的元素法 第六章 定积分的应用 ᵯ 2 + ᵯᵯ+ ᵯ= 0 特征方程 ᵯ″ + ᵯᵯ′ + ᵯᵯ= 0 (ᵯ,是常数) 则 ᵯ′ = ᵯeᵯᵯ ,ᵯ″ = ᵯ 2eᵯᵯ 代入方程并化简,得 这就说明:只要ᵯ满足特征方程,那么ᵯ= eᵯᵯ便是解

第六章定积分的应用+0E(是常数)1.当2-40时,特征方程有两个不相等的实根,设为则可得微分方程的两个线性无关的特解:Y1 = er1x, y2 = er2x,于是通解为y = Cierix + C2er2x.第一节定积分的元素法
第一节 定积分的元素法 第六章 定积分的应用 则可得微分方程的两个线性无关的特解: 于是通解为 特征方程有两个不相等的实根,设为ᵯ1 ,ᵯ2 , 1. 当ᵯ 2 − 4ᵯ> 0时, ᵯ″ + ᵯᵯ′ + ᵯᵯ= 0 (ᵯ,是常数) ᵯ 2 + ᵯᵯ+ ᵯ= 0