
第七节无穷小的比较一、无穷小的比较二、等价无穷小代换
一、无穷小的比较 二、等价无穷小代换 第七节 无穷小的比较
第一章函数与极限一、无穷小阶的比较在自变量统一变化过程中,两个无穷小之和、差、积仍为无穷小思考:两个无穷小之商是否还是无穷小?1t31-sin xxcos x=0Tlimlimlimlim -82x=0x2x2xx→0x-0 xx-→00.15反映出无穷小量趋于零的0.150.05快慢程度不一样!0.40.20.20.40.05/-0.11第七节无穷小的比较
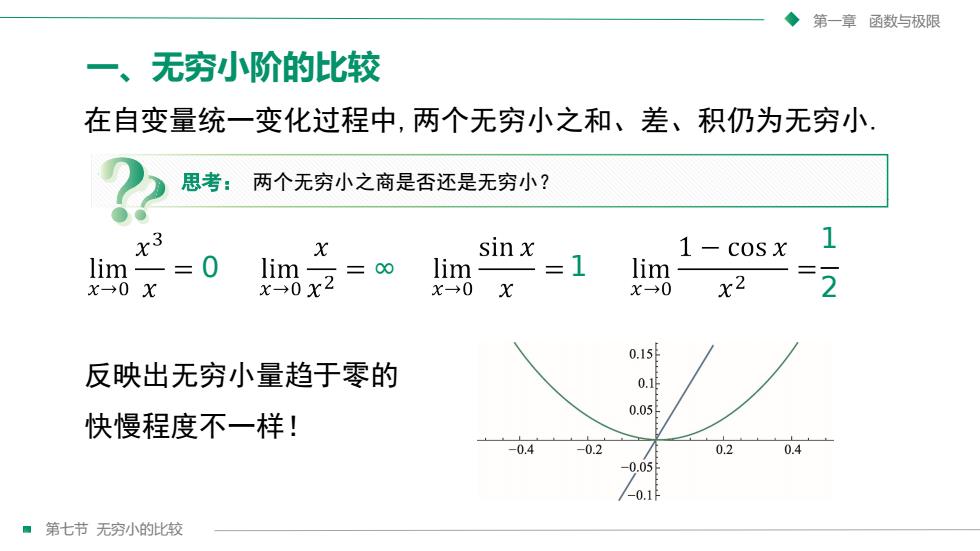
第七节 无穷小的比较 第一章 函数与极限 一、无穷小阶的比较 在自变量统一变化过程中,两个无穷小之和、差、积仍为无穷小. 反映出无穷小量趋于零的 快慢程度不一样! 思考: 两个无穷小之商是否还是无穷小? 0 ∞ 1 1 2

第一章函数与极限定义设α和β是同一自变量变化过程中的无穷小量且α≠0β(1)如果lim=0,则称β是比α高阶的无穷小,记作β=o(α);-αB(2)如果lim=80,则称β是比α低阶的无穷小αB(3)如果limC≠0,则称β与α是同阶无穷小二αβ特别地,如果lim==1,则称β与α是等价无穷小,记作α~βaβ(4)如果lim=C≠0,k>0,则称β是关于α的k阶无穷小qk第七节无穷小的比较
第七节 无穷小的比较 第一章 函数与极限 定义 设α和β是同一自变量变化过程中的无穷小量,且α ≠ 0. 则称β是比α 高阶的无穷小, 低阶的无穷小; 同阶无穷小; 则称β是比α 则称β与α是 则称β是关于α的 则称β与α是 记作 α~β. 记作 β=o(α);

第一章函数与极限例如:x3= 0,:×→0时,x3是x的高阶无穷小,即x3=0(x): limx→0 xx:x→0时,x是x2的低阶无穷小;: lim8,x=0 x2sinx:x→0时,sinx是x的等价无穷小,即sin日口1:limxx-011- cosx:x→0时,1一cosx是x2的同阶无穷小: lim2'x2x-→01一cosx是x的二阶无穷小11-cosx~L-121 - cos x是x?的等价无穷小,2第七节无穷小的比较
第七节 无穷小的比较 第一章 函数与极限 例如: 即 sinᵼ~ᵼ; 第七节 无穷小的比较 第一章 函数与极限

第一章函数与极限例1证明:当x→ 0时,"/1+x-1~=x.nN1+x-10证lim型an-bn=(a-b)(an-1+an-2b+...+abn-2+bn-1)Xx-00n("V1+x)"-1=limx~02("V1 + x)n-1 + ("1 +x)n=2 + . + 1n=lim1x=0 ("/1 + x)n-1 + ("V1+ x)++11:当x→0时,"1+x-1~=x.n第七节无穷小的比较
第七节 无穷小的比较 第一章 函数与极限 例1 证