
第八节函数的连续性与间断点函数的连续性函数的间断点
第八节 函数的连续性与间断点 一、函数的连续性 二、函数的间断点
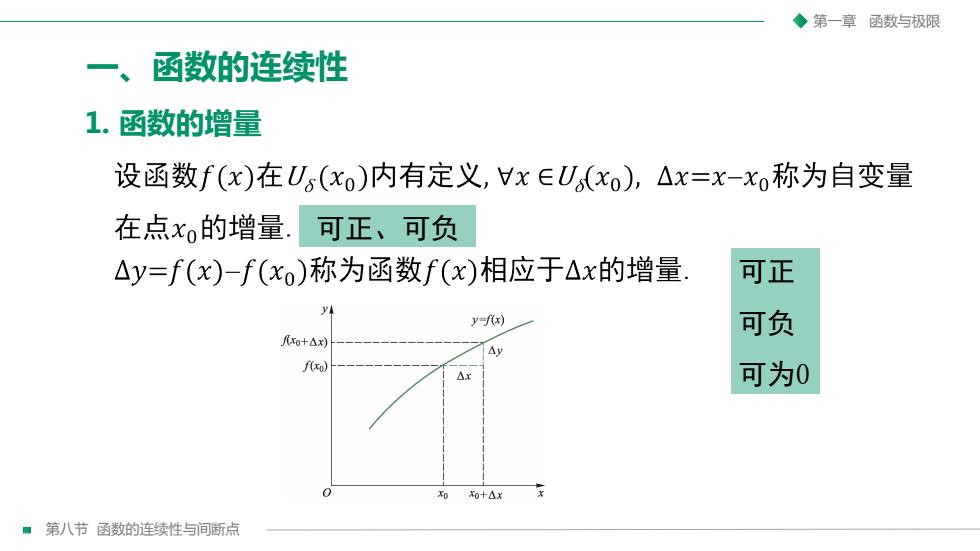
第一章函数与极限一、函数的连续性1.函数的增量设函数f(x)在U.(xo)内有定义,VxEU(xo),△x=x-x称为自变量在点xo的增量可正、可负可正△y=f(x)-f(xo)称为函数f(x)相应于△x的增量y4可负y-f(x)xo+Ax)Ayf(xo)可为0Ax0XoXo+Ax第八节函数的连续性与间断点
第八节 函数的连续性与间断点 第一章 函数与极限 一、函数的连续性 1. 函数的增量 可正、可负 可正 可负 可为0

第一章函数与极限2.连续的定义设函数y=f(x)在点x。的某一邻域内有定义,如果limAy=lim[f(xo+x)-f(xo))=0,Ax-0AX-定义1那么称函数y=f(x)在点x连续设x=xo+x,则△x-0即x→xo,Ay→0即f(x)→f(xo)设函数y=fx)在点x的某一邻域内有定义,如果limf(x)=f(xo),定义2x-xo那么称函数y=f(x)在点x连续2-定:0当x-xo<s时,恒有f(x)-f(xo)<s第八节函数的连续性与间断点
第八节 函数的连续性与间断点 第一章 函数与极限 定义2 定义1 2. 连续的定义

第一章函数与极限可见,函数f(x)在点xo连续,必须同时满足如下三个条件:(1)f(x)在点xo有定义,即f(xo)存在;(2)f(x)在点xo有极限,即limf(x)存在;X-(3)f(x)在点xo的极限值等于函数值,即limf(x)=f(xo)x→xolimf(x)=f(xo)即:f(x)在x连续←X-X1sin0,例如:函数f(x)在x=0处连续0,F0第八节函数的连续性与间断点
第八节 函数的连续性与间断点 第一章 函数与极限 例如: ᵆsin 1 ᵆ , ᵆ≠ 0, 0, ᵆ= 0

第一章函数与极限3.单侧连续如果函数f(x)在(a,xol内有定义,且 lim_f(x)=f(xo)X-x0则称f(x)在点xo处左连续如果函数f(x)在[xo,b)内有定义,且limf(x)=f(xo),x→x0则称f(x)在点xo处右连续定理函数f(x)在xo处连续-f(x)在xo处既左连续又右连续即:f(x)在xo连续limf(x)=limf(x)=f(xo)X-x0X→x0第八节函数的连续性与间断点
第八节 函数的连续性与间断点 第一章 函数与极限 3. 单侧连续 定理 第八节 函数的连续性与间断点 第一章 函数与极限