
第三章复变函数的积分1、复积分2、柯西积分定理3、柯西积分公式4、高阶导数公式5、更多的推论
* 第三章 复变函数的积分 1、复积分 3、柯西积分公式 2、柯西积分定理 4、高阶导数公式 5、更多的推论

83.1复变函数的积分1、复积分的定义2、复积分的基本性质3、复积分的计算4、小结与思考
§3.1 复变函数的积分 1、复积分的定义 2、复积分的基本性质 4、小结与思考 3、复积分的计算

1.复变函数积分的概念设C为平面上给定的一条连续曲线,如果选定C的两个可能方向中的一个作为正方向(或正向),那么我们就把C理解为带有方向的曲线,称为有向曲线如果A到B作为曲线C的正向那么B到A就是曲线C的负向记为C-.关于曲线方向的说明以后把两个端点中的一个作为起点,另一个作为终点,除特殊声明外,正方向总是指从起点到终点的方向
* 1. 复变函数积分的概念 设 C 为平面上给定的一条连续曲线, 如果 选定 C 的两个可能方向中的一个作为正方向 (或正向), 那么我们就把 C 理解为带有方向的 曲线, 称为有向曲线。 A 如果 A 到 B 作为曲线 C 的正向, B 那么 B 到 A 就是曲线 C 的负向, . − 记为C 关于曲线方向的说明: 以后把两个端点中的一个作为起点, 另一个作为终 点, 除特殊声明外, 正方向总是指从起点到终点的方向

注意:简单闭曲线C的正向是指当曲线上的点P沿此方向前进时,邻近P点的曲线的内部始终位于P点的左方。与之相反的方向就是曲线的负方向
* 简单闭曲线 C 的正向 是指当曲线上的点 P 沿此 方向前进时, 邻近 P 点的曲 线的内部始终位于 P 点的 左方. 与之相反的方向就是曲线的负方向. 注意:
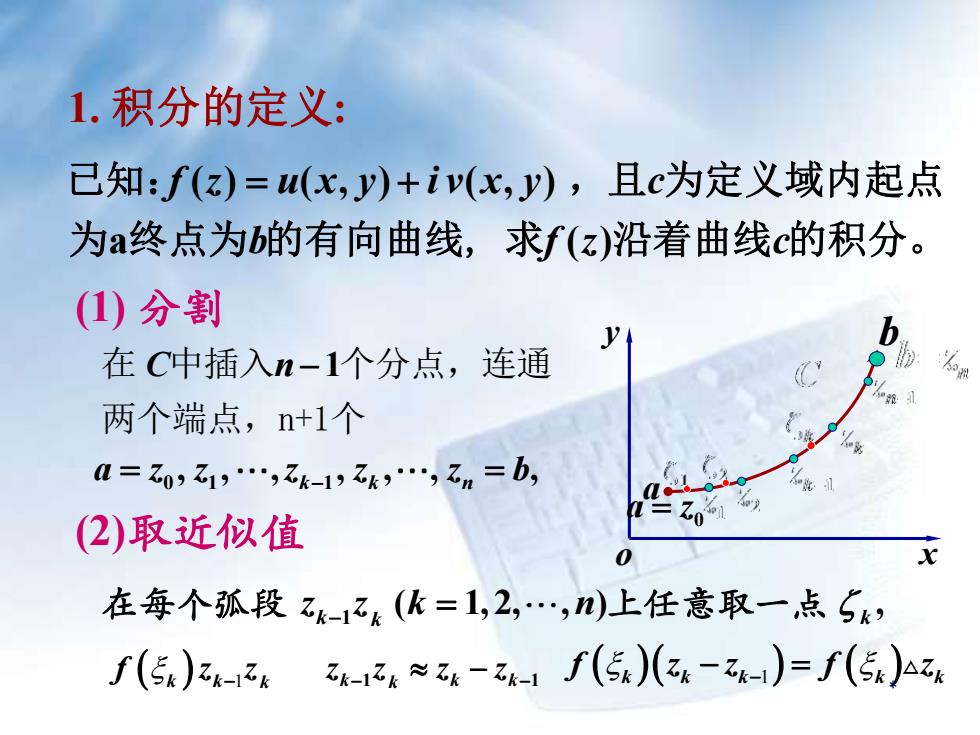
1.积分的定义:已知:f(z)=u(x,y)+iv(x,y),且c为定义域内起点为a终点为的有向曲线,求f(z)沿着曲线c的积分。(1) 分割b2在C中插入n一1个分点,连通l两个端点,n+1个Na = Zo, Z1,""",Zk-1, Zk,*.-, Zn = b,l(2)取近似值x0在每个弧段 zk-1Zk (k = 1,2,,n)上任意取一点 SkZk-12k ~ zk - Zk-1 J(5k)(zk-Zk-I)= f(5k)azkf(5k)zk-13k
* 1. 积分的定义: o x y a b 1 ( 1,2, , ) , k k k z z k n 在每个弧段 − = 上任意取一点 在 1 C n 中插入 − 个分点,连通 两个端点,n+1个 (1) 分割 (2)取近似值 0 a z = ( ) ( , ) ( , ) a ( ) f z u x y i v x y c b f z c 已知: = + ,且 为定义域内起点 为 终点为 的有向曲线, 求 沿着曲线 的积分。 ( k k ) 1 k f z z − k k k 1 1 k z z z z − − − f z z f z ( k k k k k )( − = −1 ) ( ) 0 1 1 , , , , , , , k k n a z z z z z b = = −