
高等数学第八版同济大学数学科学学院编
高等数学 第八版 同济大学数学科学学院 编
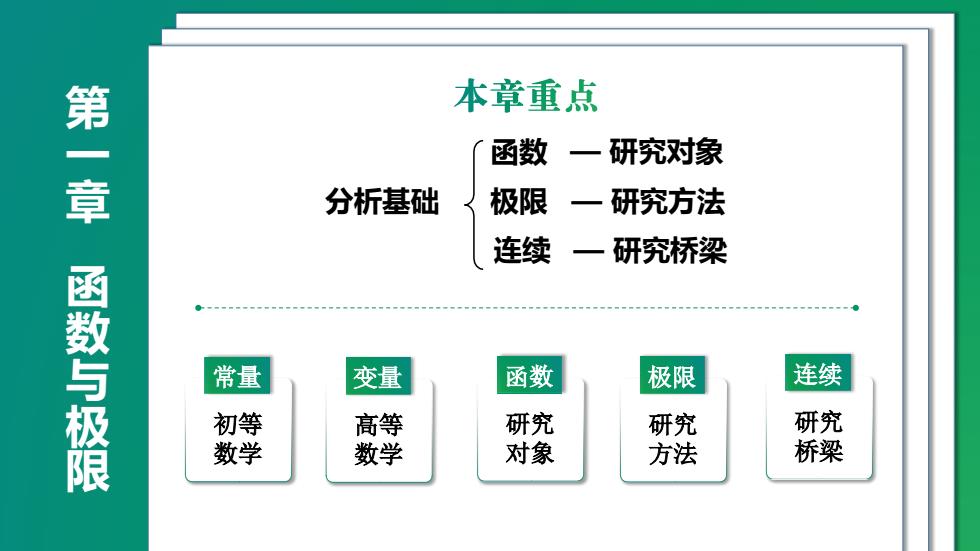
本章重点第一章函数一研究对象分析基础极限一研究方法连续一研究桥梁函数与极限连续函数常量极限变量研究初等研究高等研究桥梁数学数学对象方法
第一章函数与极限 分析基础 函数 极限 连续 — 研究对象 — 研究方法 — 研究桥梁 常量 初等 数学 变量 高等 数学 函数 研究 对象 极限 研究 方法 连续 研究 桥梁

目录第一章CONTENTS第一节映射与函数第二节数列的极限第四节第三节函数的极限无穷小与无穷大第六节第五节极限运算法则极限存在准则两个重要极限第八节第七节函数的连续性与间断点无穷小的比较第九节第十节「连续函数的运算与初等闭区间上连续函数的性质函数的连续性
CONTENTS 目 录 第一章 第一节 映射与函数 第三节 函数的极限 第二节 数列的极限 第四节 无穷小与无穷大 第五节 极限运算法则 第七节 无穷小的比较 第六节 极限存在准则 两个重要极限 第八节 函数的连续性与间断点 第九节 连续函数的运算与初等 函数的连续性 第十节 闭区间上连续函数的性质

第二节数列的极限一、数列极限的定义二、 收敛数列的性质
第二节 数列的极限 一、数列极限的定义 二、收敛数列的性质

第一章函数与极限一、数列极限的定义1.两个引例1)引例1(割圆术)“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣-刘徽它包含了“用已知逼近未知,用近似逼近精确的重要极限思想第二节数列的极限
第二节 数列的极限 第一章 函数与极限 一、数列极限的定义 1)引例1(割圆术) 1. 两个引例 它包含了“用已知逼近未知, 用近似逼近精确”的重要极限思想