
第二章解析函数2.1复变函数2.2导数与解析函数2.3初等函数
第二章 解析函数 2.1 复变函数 2.2 导数与解析函数 2.3 初等函数

S 2. 1 复变函数复变函数的基本概念复变函数的极限复变函数的连续
* ◼ 复变函数的基本概念 ◼ 复变函数的极限 ◼ 复变函数的连续 §2.1 复变函数

82.1.1复变函数的基本概念定义2.1设E为一复数集.若对E中的每一个复数z=x+iy按照某种法则有确定的一个或几个复数w=u+iv与之对应,那么称是定义E上的复变数的函数(简称复变函数),记作W=f(E称为定义域,E中所有的对应的一切w值构成的集合称为的值域,记作E).f(E)={WEzEE,f(z)=W)12Rez ImzznargzArgz
§2.1.1 复变函数的基本概念 定义2.1 设E为一复数集.若对E中的每一个复数 ,按照某种法则f有确定的一个或几个复数 与之 对应,那么称f是定义E上的复变数z的函数(简称复变 函数),记作 . z x y = + i w u v = +i w f z = ( ) f E w z E f z w ( ) { | , ( ) } = = E称为定义域. E中所有的z对应的一切w值构成的集合称 为f的值域,记作 f(E)

例函数W=z令z=x+iy,w=u+iv,则 u+iv =(x+iy)?=x?- y? +2xyi,于是函数w=z对应于两个二元实变函数:u=x?-y2, v=2xy.它们确定了自变量为和√的两个二元实变函数
例 , 2 函数w = z 令 z = x + iy, w = u + iv, 2 则 u + iv = (x + iy) 2 , 2 2 = x − y + xyi : 于是函数 w = z2 对应于两个二元实变函数 , 2 2 u = x − y v = 2xy. 它们确定了自变量为x 和 y的两个二元实变函数. 4
复变函数的几何意义对于复变函数w=/=)即u+iv=(x+iy),可以理解为两个复平面上的点集之间的映射2平面w平面EZ1WW= f(z)Z+x0u.今后不再区别函数与映射
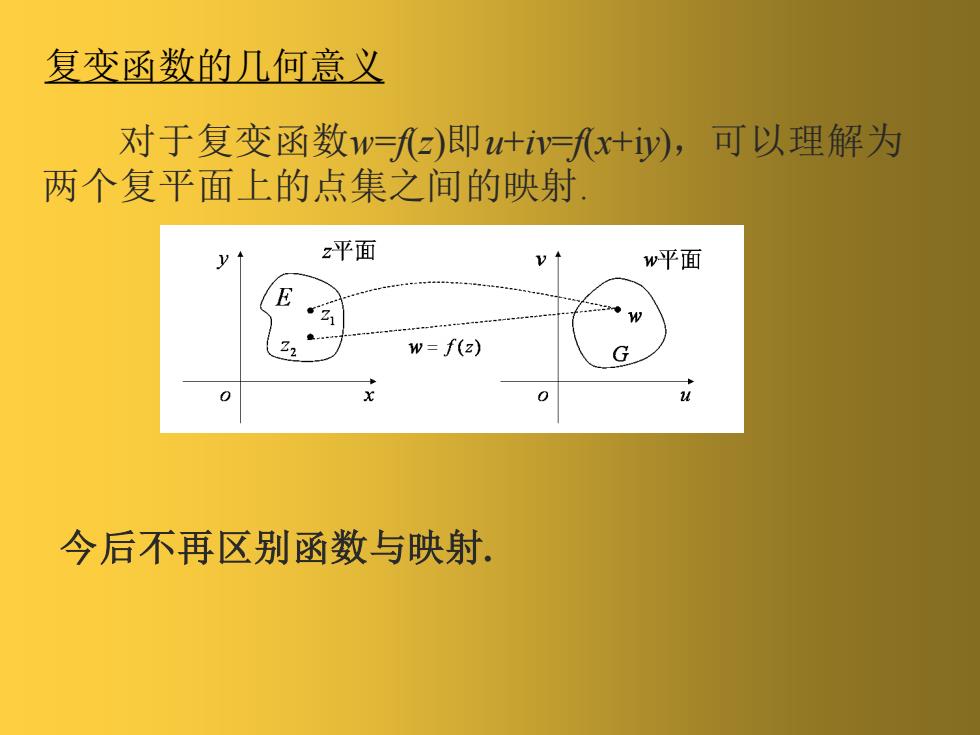
对于复变函数w=f(z)即u+iv=f(x+iy),可以理解为 两个复平面上的点集之间的映射. 复变函数的几何意义 今后不再区别函数与映射