
(F,G) ■(F,G) □(F,G) □(y,z) M ☐(z,x) M ☐(x,y) M 则在点M(x,yo,z0)有 x□x0 切线方程 y□yo z□z0 [F,G) [F,G) (F,G) y,z) M (z,x) M (x,y) M 法平面方程 (F,G) (y,z) ()C) z,x) (y o) M (F,G) (z☐z0)□0 (x,y) M
则在点 切线方程 法平面方程 有 或

法平面方程 [F,G) (yz) M) [F,G) z,x) m(EYo) (F,G) K,)w(202o)☐0 也可表为 x□x0 y口y0 z□20 Fx(M)F(M)F2(M) ▣0 Gx(M)Gy(M)G2(M)
也可表为 法平面方程
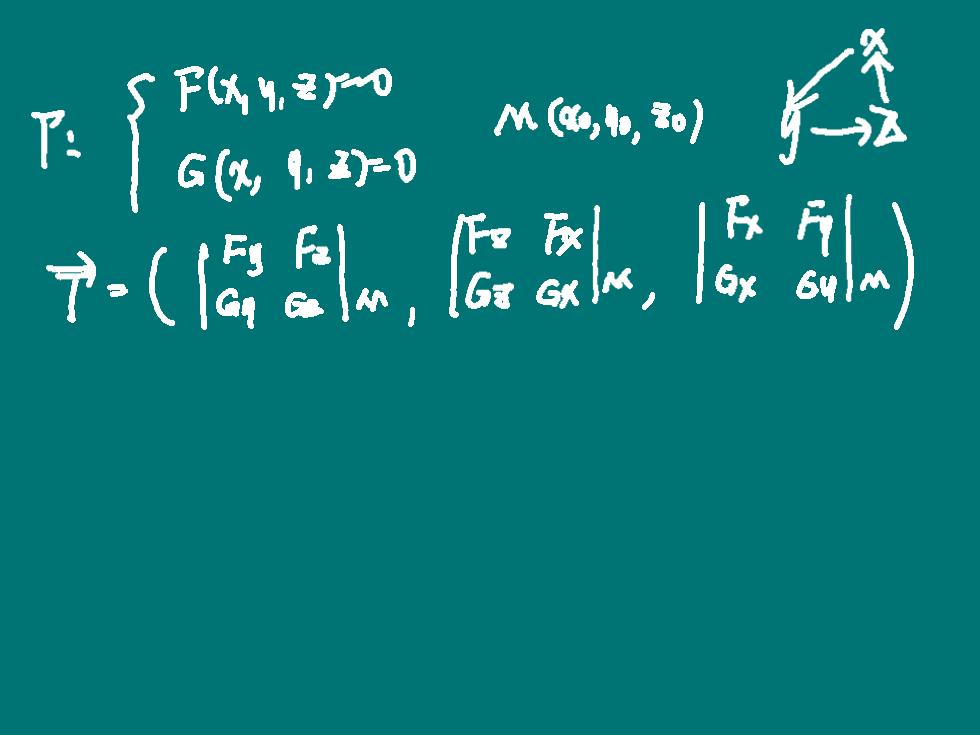
tar M,o) -(悟,层,1及)

例2.求曲线x2口y2口z2口6,x口y□z口0在点 M(1,-2,1)处的切线方程与法平面方程 解法1令F口x2口y2口z2,G口x□y口z,则 (F,G) 2y 2z □2(y0z) ☐6; ■(y,2) M 11 M M ☐(F,G) 00: (F,G) ☐6 ☐(z,x) M ☐(x,y) M 切向量 T☐(☐6,0,6) 2rg Xx口z□2□0 切线方程 06 即 y□2日0
例2. 求曲线 在点 M ( 1,–2, 1) 处的切线方程与法平面方程. 切线方程 解法1 令 则 即 切向量

法平面方程 口6(x☐1)☐0(y口2)口6(z▣1)▣0 即 x□z☐0 dz 解法2.方程组两边对x求导,得 dx d dz 01 dx □x 解得 dy z口x dz 01 x□y dx y□z dx y□z 1 1 1 曲线在点M(1,-2,1)处有: 切向量 dz 女 ☐1,0,□1)
法平面方程 即 解法2. 方程组两边对 x 求导, 得 曲线在点 M(1,–2, 1) 处有: 切向量 解得