
Advanced mathematics 第七章 高等数学 多元函数积分学 人民邮电出版社
1 第七章 多元函数积分学 第七章 人民邮电出版社 Advanced mathematics 高等数学 多元函数积分学

第七章 内容导航 第一节二重积分的概念、计算和应用 第二节三重积分的概念、计算和应用 第三节对弧长的曲线积分与对坐标的曲线积分 第四节对面积的曲面积分与对坐标的曲面积分 第五节格林公式、高斯公式和斯托克斯公式
2 第七章 多元函数积分学 第七章 内容导航 第二节 三重积分的概念、计算和应用 第三节 对弧长的曲线积分与对坐标的曲线积分 第四节 对面积的曲面积分与对坐标的曲面积分 第一节 二重积分的概念、计算和应用 第五节 格林公式、高斯公式和斯托克斯公式
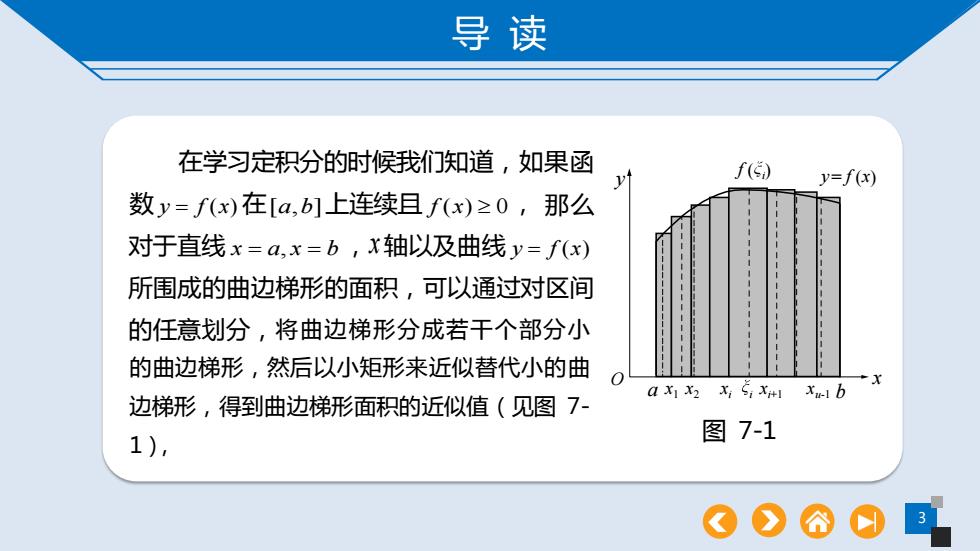
导读 在学习定积分的时候我们知道,如果函 f() y=f(x) 数y=f(x)在[a,b]上连续且f(x)≥0,那么 对于直线x=a,x=b,x轴以及曲线y=f(x) 所围成的曲边梯形的面积,可以通过对区间 的任意划分,将曲边梯形分成若干个部分小 的曲边梯形,然后以小矩形来近似替代小的曲 0 -x a X1 X2 Xi Sixit xu1b 边梯形,得到曲边梯形面积的近似值(见图7 1), 图7-1
导 读 3 图 7-1 在学习定积分的时候我们知道,如果函 数 y f x = ( ) 在[ , ] a b 上连续且 f x( ) 0 , 将曲边梯形分成若干个部分小 的曲边梯形,然后以小矩形来近似替代小的曲 边梯形,得到曲边梯形面积的近似值(见图 7- 1), 那 么 对于直线 x a x b = = , ,x 轴以及曲线 y f x = ( ) 所围成的曲边梯形的面积,可以通过对区间 的任意划分, y O x a x1 x2 xi i f ( i ) y= f (x) xi+1 xu-1 b
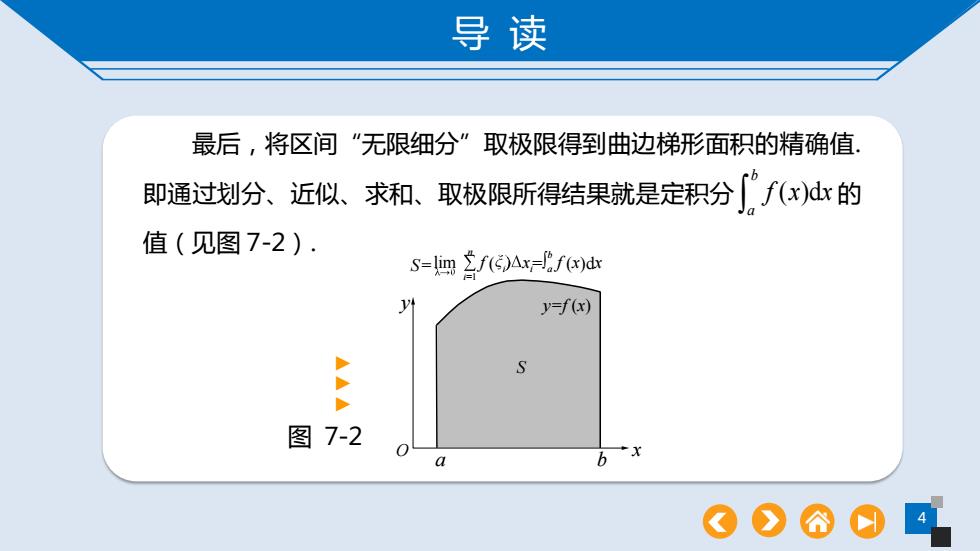
导读 最后,将区间“无限细分”取极限得到曲边梯形面积的精确值 即通过划分、近似、求和、取极限所得结果就是定积分「”f(x)dx的 值(见图7-2). Sm()Axf()dx y=f(x) P S 图7-2 a bx
导 读 4 最后,将区间“无限细分”取极限得到曲边梯形面积的精确值. 即通过划分、近似、求和、取极限所得结果就是定积分 ( )d b a f x x 的 值(见 图 7-2). O S y=f (x) a b x y S=lim f ( i xi= b a f (x)dx n i=1 图 7-2 ▲▲▲
导读 作为一元函数的定积分有许多应用但仍有许多问题无法处理 比如,在定积分的应用中,我们计算了旋转体的体积、并作了已知 截面求体积.但对一般形状的物体,用定积分求其体积就显得困难, 因此我们需要用二重积分或三重积分来解决此类问题
导 读 5 作为一元函数的定积分有许多应用,但仍有许多问题无法处理, 比如,在定积分的应用中,我们计算了旋转体的体积、并作了已知 截面求体积.但对一般形状的物体,用定积分求其体积就显得困难. 因此我们需要用二重积分或三重积分来解决此类问题