
第三节 第六章 复合求导 隐品数求导 一元复合函数 y=f(u),u=p(x) dydy du 求导法则 dx du dx 微分法则 dy=f'(u)du=f"(u)o'(x)dx HIGH EDUCATION PRESS 机动目录上页下页返回结束
第三节 一元复合函数 求导法则 微分法则 机动 目录 上页 下页 返回 结束 复合求导 隐函数求导 第六章

多元函数复合求导 一、多元复合函数求导的链式法则 二、多元复合函数的全微分 HIGH EDUCATION PRESS
多元函数复合求导 一、多元复合函数求导的链式法则 二、多元复合函数的全微分
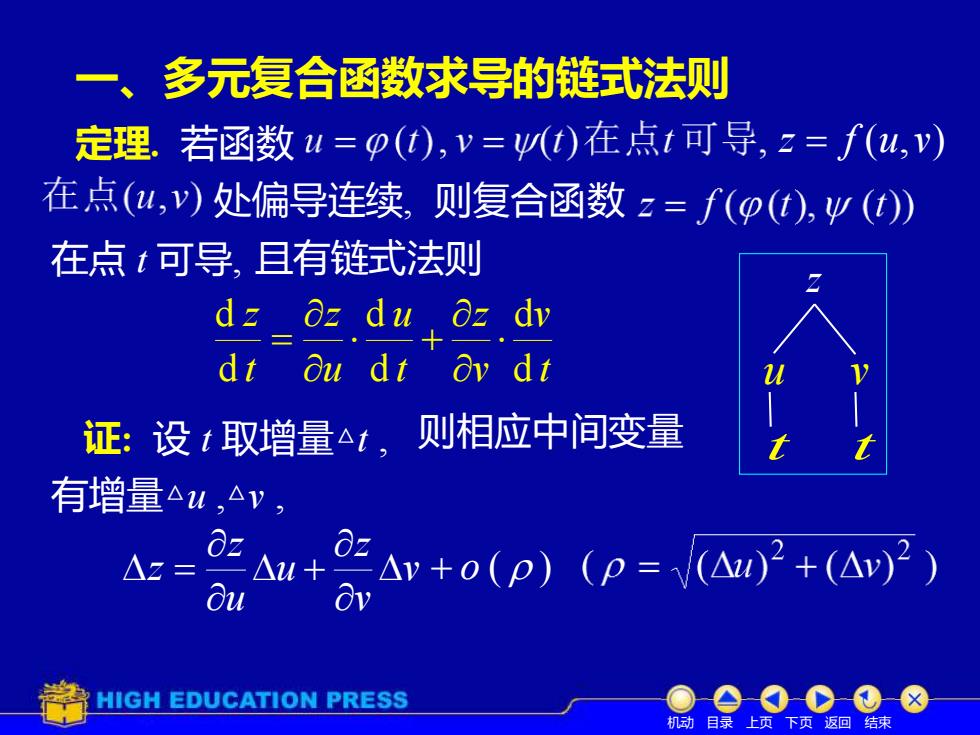
一、多元复合函数求导的链式法则 定理.若函数u=p(t),v=yW(t)在点t可导,z=f(u,v) 在点(u,v)处偏导连续,则复合函数z=f(p(t),y(t) 在点t可导,且有链式法则 dz Oz du 0z dv dt ou dt ay di 证:设t取增量△t,则相应中间变量 有增量△u,△v, △z= Bu Ar+o(p)(p=>2+(AwP) 8v HIGH EDUCATION PRESS 机动目录上页下页返回结束
一、多元复合函数求导的链式法则 定理. 若函数 z = f (u,v) 处偏导连续, 在点 t 可导, t v v z t u u z t z d d d d d d + = z 则复合函数 证: 设 t 取增量△t , v v z u u z z + = + o ( ) 则相应中间变量 且有链式法则 u v t t 机动 目录 上页 下页 返回 结束 有增量△u , △v

△z aAu+2△y+o(p) (p=V(△)2+(△)2) △tO2u△t v△t △t 令△t→0,则有△u→0,△v→0, △udu △v.dv 11 △t dt' △t _di o(p) △t (△t<0时根式前加”-号) dz Oz du Oz dv (全导数公式) dt au di Oy dt HIGH EDUCATION PRESS 机动目录上页下页返回结束
则有u → 0, v → 0, ( 全导数公式 ) t v v z t u u z t z + = t o + ( ) z u v t t ( ( ) ( ) ) 2 2 = u + v ( ) o = (△t<0 时,根式前加“–”号) t v t v t u t u d d , d d → → 机动 目录 上页 下页 返回 结束 t v v z t u u z t z d d d d d d + =

例1设u=x,x=sn1,y=cost求 dt 解: du Gu dx Ou dy diox dt y di =xcost+x"Inx(-sint) =(sint)cos(cos2t-Insint) HIGH EDUCATION PRESS
例1 设 u x x t y t = = = y , sin , cos 求 du dt 解: du u dx u dy dt x dt y dt = + 1 cos ln ( sin ) y y yx t x x t − = + − cos 1 2 (sin ) (cos lnsin ) t t t t − = −