5.3直线及其方程一、空间直线的一般方程定义空间直线可看成两平面的交线7P,: Ax+By+Cz+D, = 0P 2 : A,x+B,y+C2z+ D, = 0Pi Ax+By+Cz+D = 011i A,x+B,J+C,z+ D, = 00空间直线的一般方程
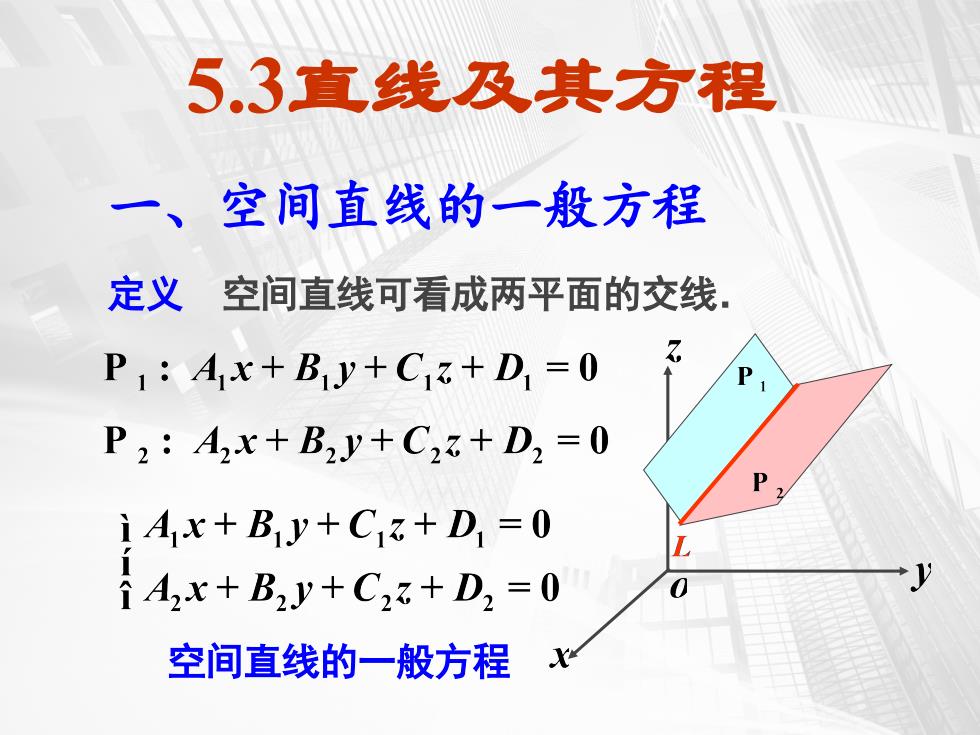
5.3直线及其方程 定义 空间直线可看成两平面的交线. 空间直线的一般方程 一、空间直线的一般方程
空间直线的对称式方程与参数方程二、方向向量的定义:如果一非零向量平行于71一条已知直线,这个向量称XMxM.为这条直线的方向向量0yM,(xo, Jo,zo),M(x,y,z),X" MI L,M,Mll ss =(m, n, p),M,M={x- Xo,y- yo,z- zo?
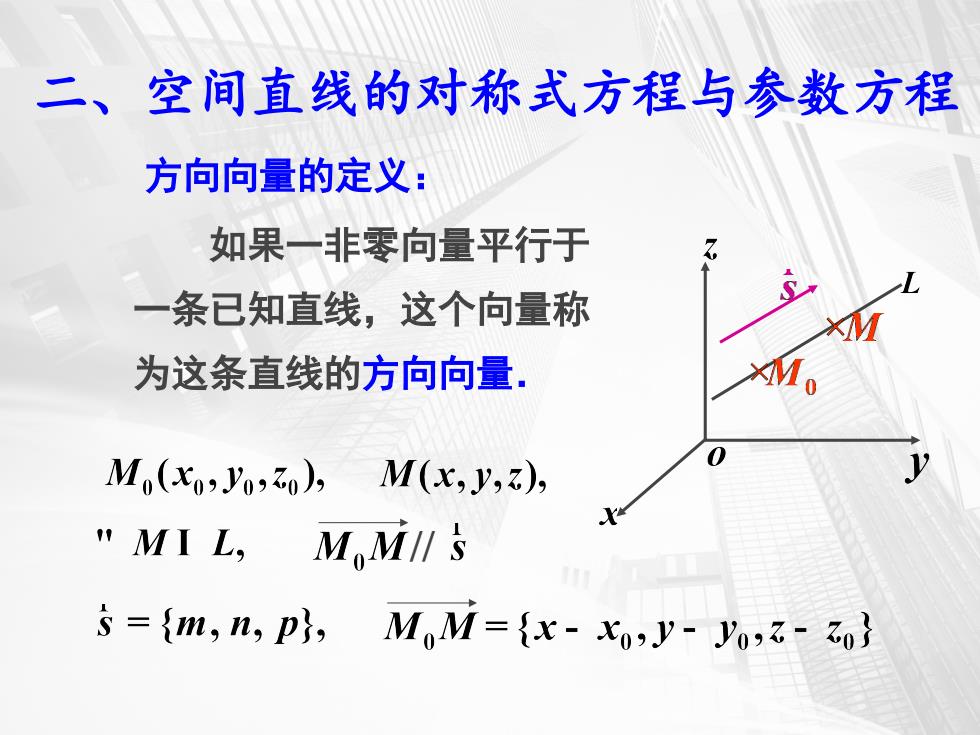
方向向量的定义: 如果一非零向量平行于 一条已知直线,这个向量称 为这条直线的方向向量. // 二、空间直线的对称式方程与参数方程
x- xo -y- yoZ-Z0直线的对称式方程mnpx- Xo0 - z- 30 = ty- Jomnp直线的一组方向数ix=x,+mtiy=yo +nt方向向量的余弦称为直线的方向余弦I z = zo + pt直线的参数方程
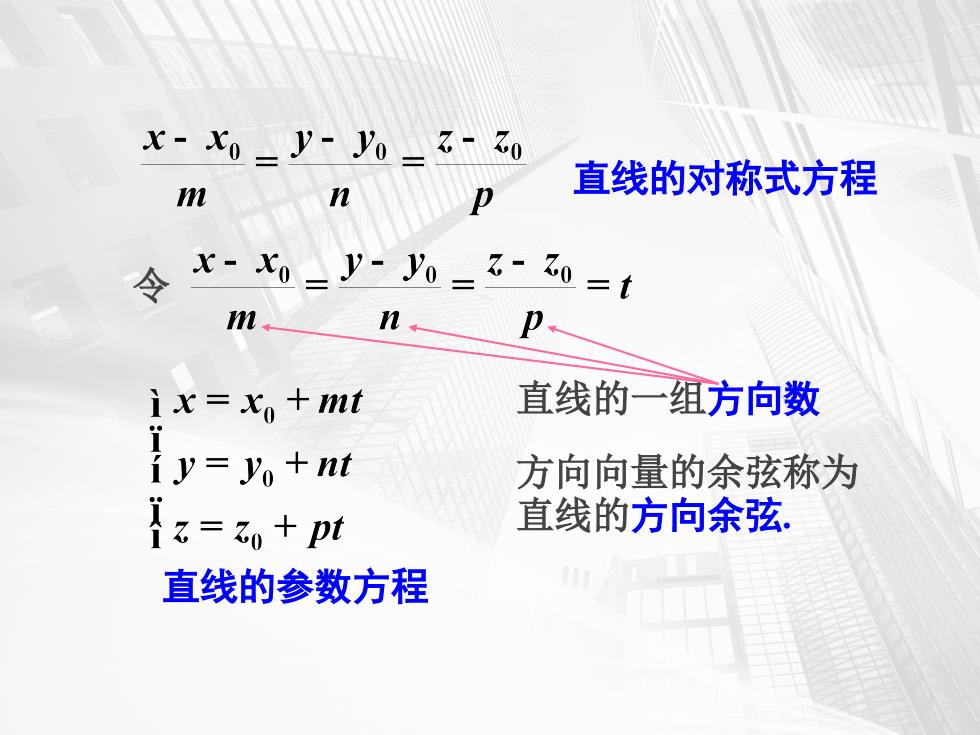
直线的对称式方程 令 直线的一组方向数 方向向量的余弦称为 直线的方向余弦. 直线的参数方程

例1求经过 M (Xi, J1,可), M, (X2, J2,2)两点的直线方程解因为直线过 M,M,两点因此可取M,M,作为直线的方向向量s = M,M, =(x2 - Xi,y2 - 1,z2 - zf}由点向式即得所求直线的方程为x- Xi - y-yi - z- ziX2 - Xi y2- Ji72 - 71直线的两点式方程
例1 求经过 两点的直线方程 解 因为直线过 两点 因此可取 作为直线的方向向量 由点向式即得所求直线的方程为 ——直线的两点式方程

例2用对称式方程及参数方程表示直线ix+v+z+1=0i2x - +3z+4=0解一用点向式在直线上任取一点(xo,yo,zo)i yo +zo +2 = 0取 x=1 iyo - 3zo - 6= 0解得 yo=0, zo=-2点坐标(1,0,-2)
例2 用对称式方程及参数方程表示直线 解一 用点向式 在直线上任取一点 取 解得 点坐标