
微分法在几何上的应用一、空间曲线的切线和法平面定义 设 M是空间曲线L上的一个定点,M*是L上的一个动点,当M*沿曲线L趋于M时,割线MM*的极限位置MT(如果极限存在)称为曲线L在M处的切线。下面我们来导出空间曲线的切线方程
微分法在几何上的应用 一、空间曲线的切线和法平面 定义 设 M是空间曲线L 上的一个定点,M* 是 L 上的一个动点,当M* 沿曲线L 趋于M 时 , 割线MM*的极限位置 MT (如果极限存在)称为曲线L在M 处的切线。 下面我们来导出空间曲线的切线方程
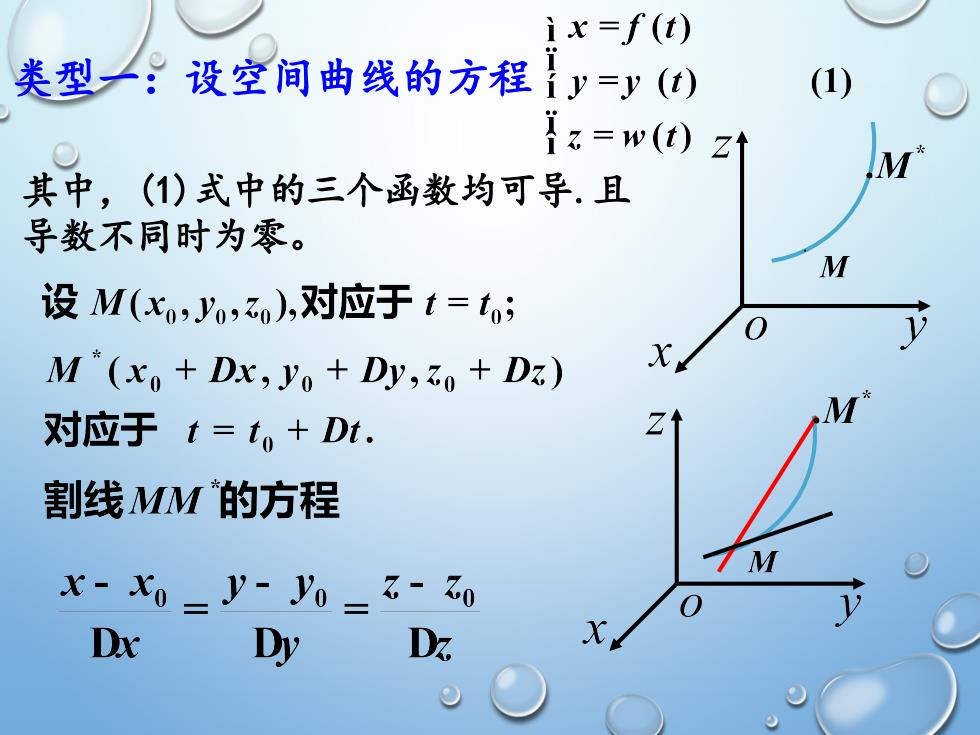
ix=f(t)类型一:设空间曲线的方程(1)iy=y (t)iz=w(t) ztM*其中,(1)式中的三个函数均可导.且导数不同时为零。M设 M(xo,Jo,zo),对应于 t = to;0LM*(xo + Dx, yo + Dy,zo + Dz)MZt对应于 t = to+ Dt.割线MM的方程MX- Xo-y- Jo- z- zoV0DxDz.Dy
类型一:设空间曲线的方程 其中,(1)式中的三个函数均可导.且 导数不同时为零

切线的过程考察割线趋近于极限位置上式分母同除以Dt.x- xo-y- o-z- zo当M*?M,即Dt?时DzDxDyDtDtDtX- Xo -J- yo - z- zo曲线在M处的切线方程fdto) y dto) wdto)切向量:切线的方向向量称为曲线的切向量T = (fdto)y d(to),wdto)法平面:过M点且与切线垂直的平面fto)(x- xo)+y to)(y- yo)+wdto)(z- zo)=0
考察割线趋近于极限位置——切线的过程 上式分母同除以 曲线在M处的切线方程 切向量:切线的方向向量称为曲线的切向量. 法平面:过M0点且与切线垂直的平面

例1求曲线口:解 当t=0时,x=0,=1,z=2,xe=e' cost, ye= 2cost - sint, ze=3e3tIxd0) =1, y(0) = 2, zd(0)=3,x-0y-1z-2切线方程23x+2(V-1)+3(z-2)=0法平面方程即x+2+3z-8=0
解 切线方程 法平面方程

iy=f(x)类型二:空间曲线方程i取x为参数iz=y (x)在M (xo, yo,zo)处,X- Xo-y- Jo- z- zo切线方程为fdx) y dx)1法平面方程为(x- x)+fdx)(y- yo)+y x)(z- zo)=0F(x,y,z)= 0类型三:空间曲线方程G(x,y,z) = 0六切向量-GGGG
类型二:空间曲线方程 取x为参数 法平面方程为 类型三:空间曲线方程 切向量