
第五章,向量与空间解析几何第一节向量及其运算
第五章 向量与空间解析几何 第一节 向量及其运算

空间直角坐标系本章先引入空间直角坐标系,把点和有序数组、空间图形和代数方程联系起来,建立起对应关系,给数和代数方程以几何直观意义,从而可以利用代数方法研究空间图形的性质和相互关系;接着介绍向量概念,然后以向量代数为工具,重点讨论空间基本图类平面,直线,常用的曲面和曲线
一、空间直角坐标系 本章先引入空间直角坐标系,把点和有序数 组、空间图形和代数方程联系起来,建立起 对应关系,给数和代数方程以几何直观意义, 从而可以利用代数方法研究空间图形的性质 和相互关系;接着介绍向量概念,然后以向 量代数为工具,重点讨论空间基本图类—— 平面,直线,常用的曲面和曲线

1、空间点的直角坐标竖轴三个坐标轴的正方向符合右手法则。即以右手握住z轴,当右手的四个手指定点从正向x轴以"角2度转向正向V轴横轴x时,大拇指的指向空间直角坐标系就是z轴的正向
横轴 x y 纵轴 z 竖轴 定点 o 空间直角坐标系 三个坐标轴的正方向符 合右手法则。 即以右手握住z 轴, 当右手的四个手指 从正向x 轴以 2 角 度转向正向y 轴 时,大拇指的指向 就是z轴的正向. 1、空间点的直角坐标
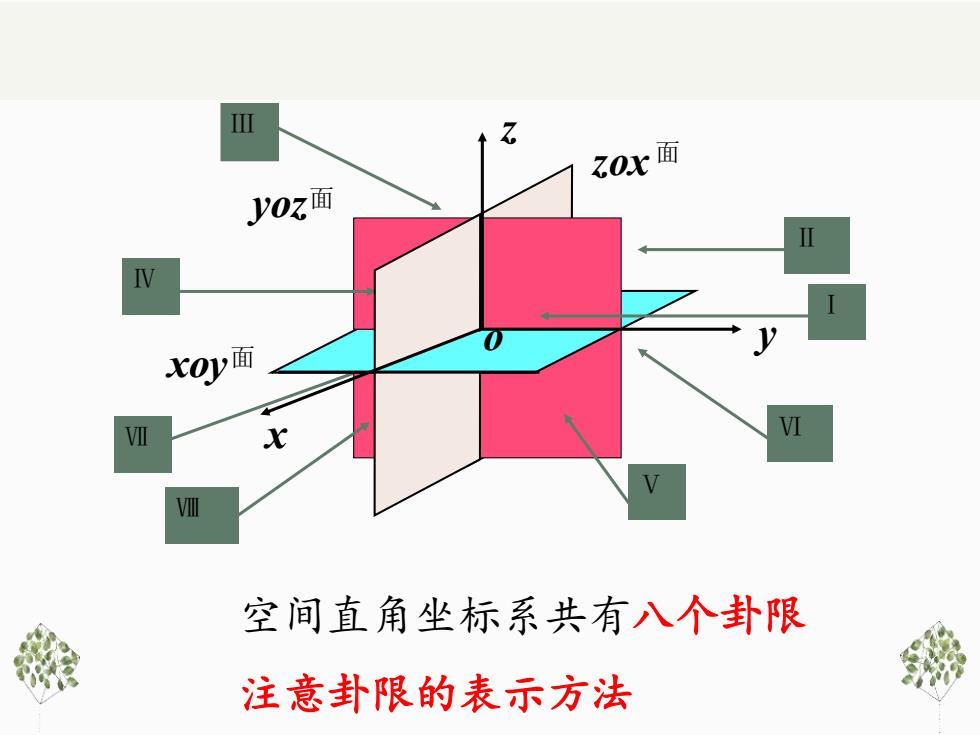
中zox面yoz面IIIV2xoy面VIVIxVIII空间直角坐标系共有八个卦限注意卦限的表示方法
Ⅶ x o y z xoy 面 yoz 面 zox 面 空间直角坐标系共有八个卦限 注意卦限的表示方法 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅷ
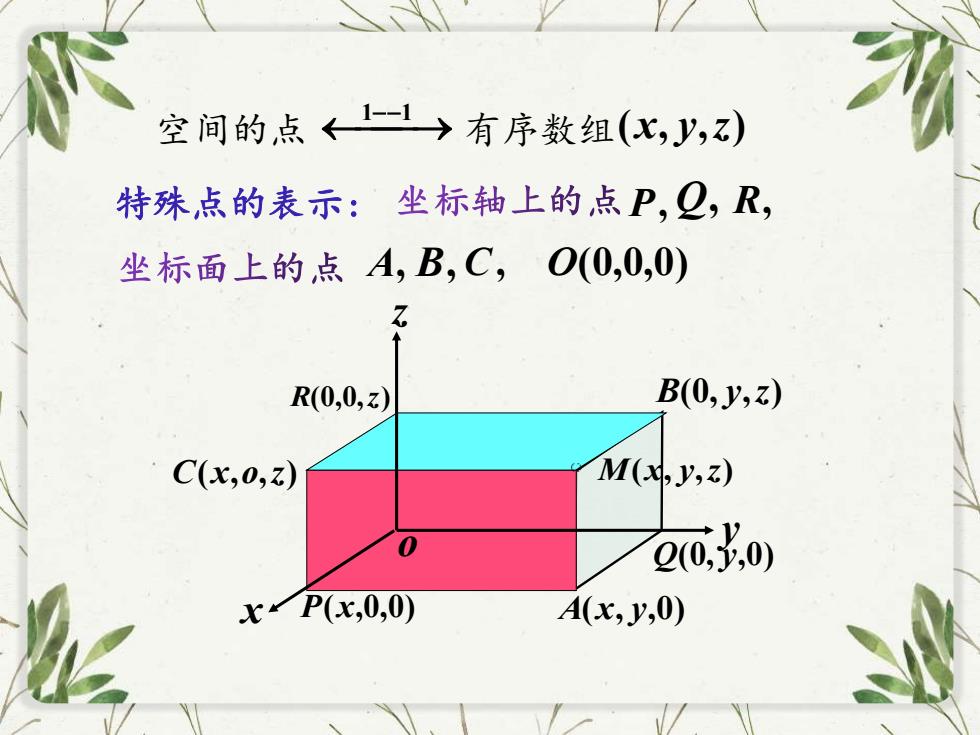
1空间的点 <l--l>有序数组(x,y,z)特殊点的表示:坐标轴上的点P,Q,R坐标面上的点 A,B,C, O(0,0,0)ZB(0,y,z)R(0,0,z)M(x,y,z)C(x,0,z)@(0,y,0)0xP(x,0,0)A(x,y,0)
空间的点 ⎯→ 有序数组 (x, y,z) 1−−1 特殊点的表示: O(0,0,0) M(x, y,z) x y z o P(x,0,0) Q(0, y,0) R(0,0,z) A(x, y,0) B(0, y,z) C(x,o,z) P, Q, R, A, B, C