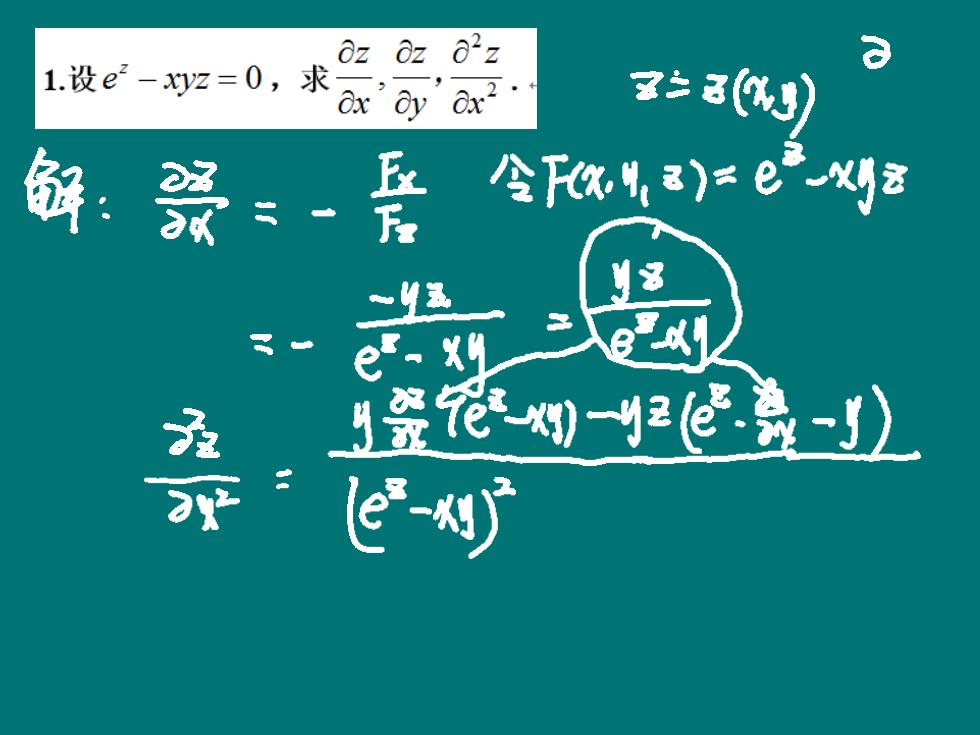
az0z∂2z 1.设e2-z=0,求 'y'6x2· 则) 解: 南 你4,)eX e-x 签径-) or

定理2.若函数F(x,y,z)满足 ①在点P(x0,yo,z)的某邻域内具有连续偏导数, ②F(x0,y0,20)☐0 ③F2(x0,y0,20)☐0 则方程F(x,y,z)口0在点(xo,yo)某一邻域内可唯一确 定一个单值连续函数z=f(x,y),满足0口f(xo,y0) 并有连续偏导数
定理2 . 若函数 的某邻域内具有连续偏导数 , 则方程 在点 并有连续偏导数 定一个单值连续函数 z = f (x , y) , 满足 ① 在点 满足: ② ③ 某一邻域内可唯一确

定理3.设函数F(x,y,山,y),G(x,y,u,)满足: ①在点P(xo,yo,o,o)的某一邻域内具有连续偏 导数; ②F(x0,y0,u0,Vo)☐0,G(x0,y0,40,o)☐0 (F,G) [u,v) 则方程组F(,y,u,)口0,G(x,y,u,)□0在点(x0,y0) 的某一邻域内可唯一确定一组满足条件40口u(xo,yo), Vo口v(xo,o)的单值连续函数u口u(x,y),V☐v(x,y)
定理3. 的某一邻域内具有连续偏 设函数 则方程组 ③ 的单值连续函数 ① 在点 ② 的某一邻域内可唯一确定一组满足条件 满足: 导数;

z=x2+y2 dy dz 2.设 +2y2+32=20求 除) 8>2以) ∫象数 J 2近6) 7) 28r4刘殷+6红蒙-0 ¥0 5紫-紫≥以 喷 名2 例费+红尝-2以

第四节 第六章 多无岛数微分学的立用 一、空间曲线的切线与法平面 二、曲面的切平面与法线 三、多元函数的极值
第四节 一、空间曲线的切线与法平面 二、曲面的切平面与法线 多元函数微分学的应用 第六章 三、多元函数的极值