
第二节数列的极限、概念的引入数列的定义三、 数列的极限四、数列极限的性质五、小结
第二节 数列的极限 • 一、概念的引入 • 二、数列的定义 • 三、数列的极限 • 四、数列极限的性质 • 五、小结
概念的引入一、禾1、割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失-刘徽!正六边形的面积 A正十二边形的面积 AR正 6×2"-1 形的面积A,A,A,,A,,An, S
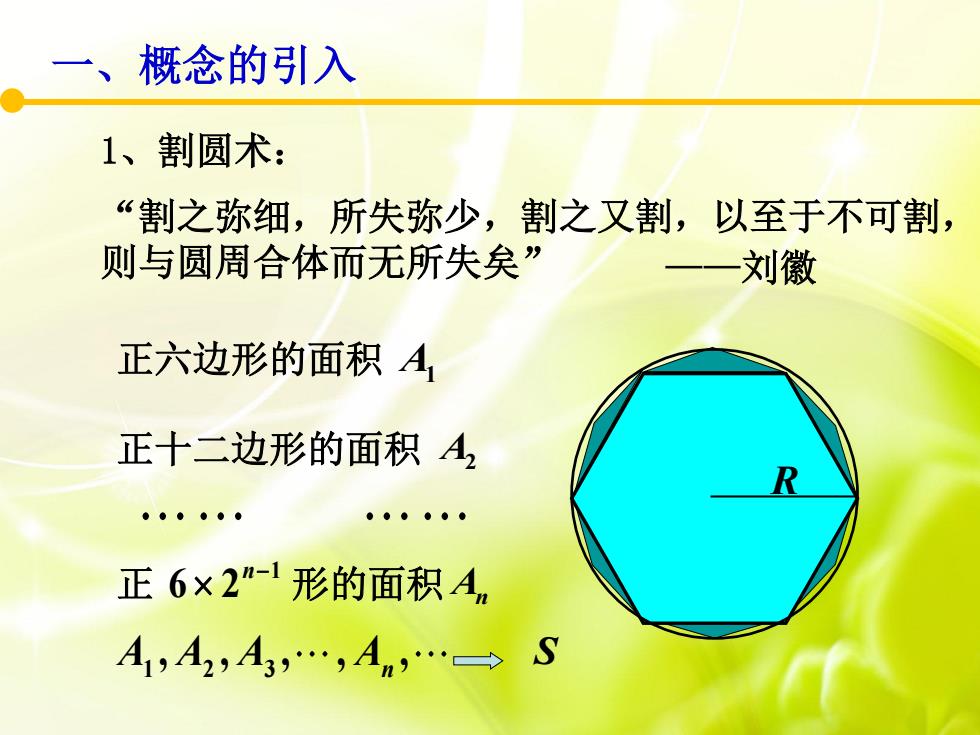
R 正六边形的面积 A1 正十二边形的面积 A2 正 形的面积 1 6 2n A n 1 2 3 , , , , , A A A A n S “割之弥细,所失弥少,割之又割,以至于不可割, 则与圆周合体而无所失矣” 1、割圆术: ——刘徽 一、概念的引入

刘徽生于公元250年左右三国后期魏国人中国古代杰出的数学家,被称为“中国数学史上的牛顿
刘 徽 生于公元250年左右 三国后期魏国人 中国古代杰出的 数学家,被称为“中 国数学史上的牛顿

2、截丈问题:“一尺之捶,日截其半,万世不竭第一天截下的杖长为X,第二天截下的杖长总和为X,2++第n天截下的杖长总和为X,=亏nHX, =1-.2n
2、截丈问题: “一尺之棰,日截其半,万世不竭” 1 1 ; 2 第一天截下的杖长为 X 2 2 1 1 ; 2 2 第二天截下的杖长总和为 X 2 1 1 1 ; 2 2 2 n n 第n X 天截下的杖长总和为 1 1 2 X n n 1

庄子庄子约前369年一前286年著名思想家,哲学家、文学家
庄 子 约前369年—前286 年 著名思想家、 哲学家、文学家