《线性代数》课程教学资源（讲稿B，高教版）第四章 特征值与特征向量 4-1 特征值与特征向量的概念与计算

第四章特征值与特征向量4-1 特征值与特征向量的概念与计算4-2 矩阵的相似对角化4-3n维向量空间的正交性4-3 实对称矩阵的相似对角化

第四章 特征值与特征向量 4-1 特征值与特征向量的概念与计算 4-2 矩阵的相似对角化 4-3 n 维向量空间的正交性 4-3 实对称矩阵的相似对角化

引入)(69)0)-(9)-2(9)计算Aα=Nα0矩阵表示一个压缩变换，它把下图中的正方形沿x轴压缩为原来的一半，02向量变换后分别与它们的原像共线0y3-1120O

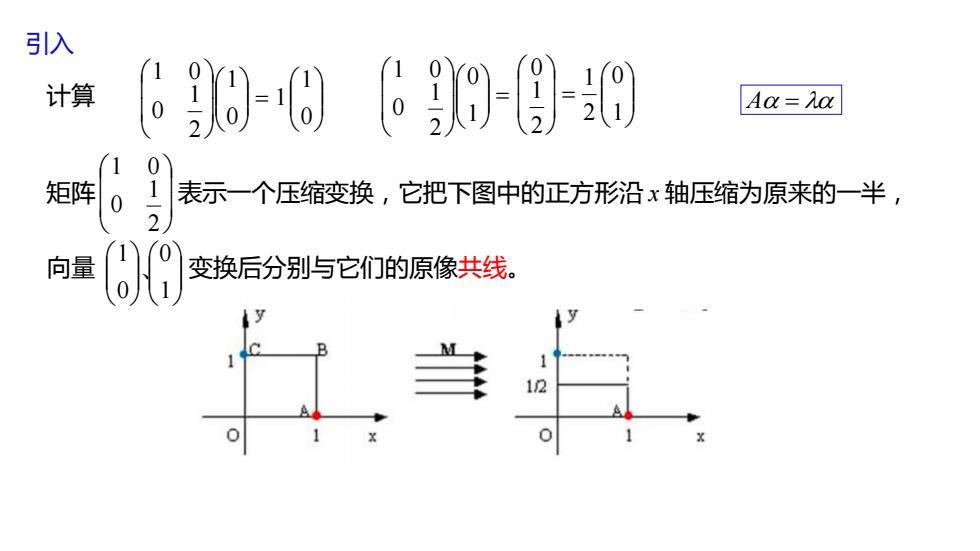
引入 计算                 0 1 2 1 0 1 0                 1 0 2 1 0 1 0         0 1 1                  1 0 2 1 2 1 0         2 1 0 1 0 矩阵 表示一个压缩变换，它把下图中的正方形沿 x 轴压缩为原来的一半， 向量   变换后分别与它们的原像共线。               1 0 0 1 、 A  

5a探究给定矩阵A=如何寻找非零向量量α及常数，使得Aα=α？CXAx,x要使例如 A=设非零向量α0(X2)[3x -2x2=2x[(3-)x -2x2 = 0只要即= Nx2X - 2x2 = 0X-23-元则有=0，即2-3元+2=0，得几=1, 21-元1[2x -2x2 = 0当=1时,得α=k1( X-x=02[x -2x =0当=2时，得α=k1[x -2x2 =0

探究 1 0 3 2          A           c d a b 给定矩阵 A ，如何寻找非零向量  及常数  ，使得 A   ？ 例如 ，设非零向量 ，要使          2 1 x x                                   2 1 2 1 2 1 1 0 3 2 x x x x x x    只要 ，即       1 2 1 2 1 3 2 x x x x x           0 (3 ) 2 0 1 2 1 2 x x x x   则有 0 ，即 ，得 1 3 2       3 2 0 2       1， 2 当  1 时， 得        0 2 2 0 1 2 1 2 x x x x          1 1 1  k 当   2 时， 得        2 0 2 0 1 2 1 2 x x x x          1 2 2  k

探究给定矩阵A：如何寻找非零向量α及常数a，使得Aα=α？矩阵的特征值与特征向量理论有着非常广泛的应用，如工程技术领域中的振动问题和稳定性问题，数学领域中方阵的对角化、微分方程的求解、线性方程组的迭代求解等

探究          c d a b 给定矩阵 A ，如何寻找非零向量  及常数  ，使得 A   ？ 矩阵的特征值与特征向量理论有着非常广泛的应用，如工程技术领域中的 振动问题和稳定性问题，数学领域中方阵的对角化、微分方程的求解、线性方 程组的迭代求解等

4-1特征值与特征向量的概念与计算定义1设A是n阶方阵，若存在常数及非零向量α，使得Aα=Nα则称2为方阵A的一个特征值，α为方阵A对应特征值α的一个特征向量注1°只对方阵考虑特征值，其特征向量是非零向量；2°若α是方阵A对应特征值2的一个特征向量，则kα也是A对应特征值2的特征向量（k≠0）A(kα)=k(Aα)= k(α)= a(kα)3°若αα..,α是A对应特征值的特征向量，则kα+kαz+.+kα,也是A对应特征值元的特征向量

4-1 特征值与特征向量的概念与计算 定义1 则称 为方阵 的一个特征值， 为方阵 对应特征值 的一个特征向量。 A   设 A 是 n 阶方阵，若存在常数  及非零向量  ，使得  A  A  注 1° 只对方阵考虑特征值，其特征向量是非零向量； 2° 若 是方阵 对应特征值 的一个特征向量，则 也是 对应特征值 的特征向量  A  k A  (k  0) A(k)  k(A)  k()  (k) 3° 若 是 对应特征值 的特征向量，则 也 是 对应特征值 的特征向量。 1 ,2 ,  ,r A  1 1 2 2 r r k  k   k  A 