《线性代数》课程教学资源（讲稿B，高教版）第一章 矩阵及其初等变换 1-4 分块矩阵

1-4分块矩阵对于行数和列数较高的矩阵A，为了简化运算，经常采用分块法，使大矩阵的运算化成小矩阵的运算.具体做法是：将矩阵A用若干条纵线和横线分成许多个小矩阵，每一个小矩阵称为A的子块，以子块为元素的形式上的矩阵称为分块矩阵例如0000012 101012-3A070

1-4 分块矩阵 对于行数和列数较高的矩阵 A, 为了简化运算，经常采用分块法，使大矩阵的 运算化成小矩阵的运算. 具体做法是: 将矩阵 A 用若干条纵线和横线分成许多个小 矩阵，每一个小矩阵称为 A 的子块，以子块为元素的形式上的矩阵称为分块矩阵. 例如            7 3 0 0 0 1 2 3 1 0 1 2          A O I A 21 12               1 2 3 0 0 1 0 1 0 1 0 0          A2 I            7 3 0 0 0 1 2 3 1 0 1 2    A1 A2 A3 A4

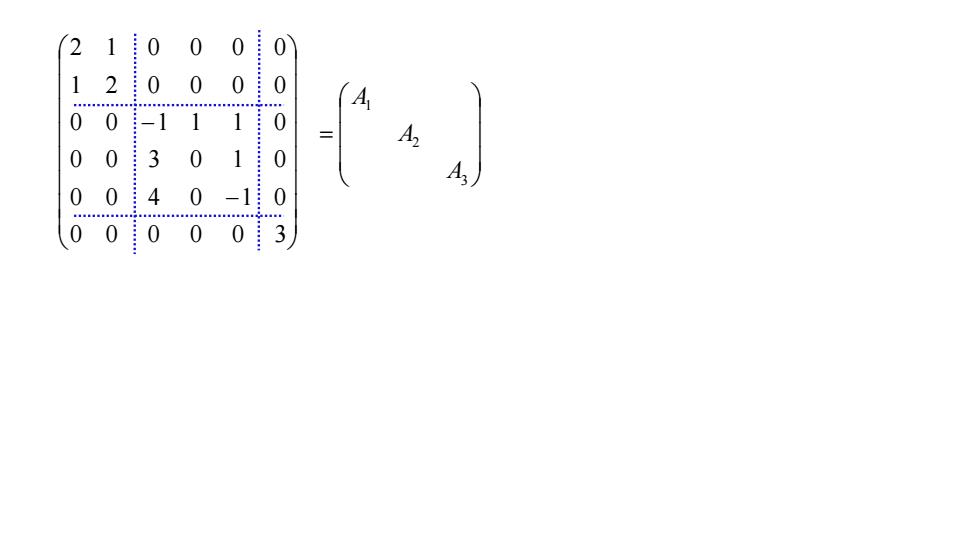
...ECR..0....0)002I002010A0001-1A,=0300...10A,40000-1.......000030

                      0 0 0 0 0 3 0 0 4 0 1 0 0 0 3 0 1 0 0 0 1 1 1 0 1 2 0 0 0 0 2 1 0 0 0 0            3 2 1 A A A

一、分块矩阵的运算1分块矩阵的加法B,B.B=设A与B是同型矩阵，且分块方法相同，A=BB.A..+Bu ... A,+B则A+B=A., + B.LA..+B.2数乘分块矩阵AKkAkA=kAkAAkA

一、分块矩阵的运算 1 分块矩阵的加法                       r r s s r r s s B B B B B A A A A A           1 1 1 1 1 1 1 1 设 A 与 B 是同型矩阵，且分块方法相同， , 则                 r r r s r s s s A B A B A B A B A B      1 1 1 1 1 1 1 1 2 数乘分块矩阵                       r r s s r r s s k A k A k A k A A A A A k A k           1 1 1 1 1 1 1 1

3.分块矩阵的转置设A是一个r×s型分块矩阵，则它的转置是一个s×r型分块矩阵。2AuA=A4/AuA2例如2A=01A21A220002:0101AfA2001则A!4A2110-12

3. 分块矩阵的转置 设 A 是一个 rs 型分块矩阵，则它的转置是一个 sr 型分块矩阵。                       T r s T s T r T T r r s s A A A A A A A A A A           1 1 1 1 1 1 1 1 ,             0 0 2 0 0 1 1 2 1 0 4 1 例如 A          21 22 11 12 A A A A 则          T T T T T A A A A A 1 2 2 2 1 1 2 1                 1 2 0 4 1 2 0 1 0 1 0 0

4.分块矩阵的乘法设矩阵A=(a,）mm,B=(b,）p，对A,B进行分块，其中A的列的分法和B的行的分法相同，则AuBu.A,B.+..A,B...A,B,+..A,Bs.B,..AB=B.BA,B.+.Ar,Bs..A,Bu, +.ABst4A

4. 分块矩阵的乘法                      s s t t r r s s B B B B A A A A AB           1 1 1 1 1 1 1 1 设矩阵 ，对 A, B 进行分块，其中A 的列的分法和 B 的 行的分法相同，则 A  aij mn B  bij np ( ) , ( )                r r s s r t r s s t s s t s s t A B A B A B A B A B A B A B A B          1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1