《线性代数》课程教学资源（讲稿B，高教版）第二章 行列式 2-2 n阶行列式的性质与计算

2-2行列式的性质和计算、行列式的性质性质1n阶行列式按任一行展开，其值相等，即det A=aiA+a2A2 +..+amAn=a,A(i=1,2,...,n)推论若行列式的某行元素全为零，则行列式的值为零。06105-13-2例1计算行列式D：2000314-30603-2解：按第二行展开D=2(-1)3+2-123-25=-2×64-341-3

2-2 行列式的性质和计算 一、行列式的性质 性质1 n 阶行列式按任一行展开，其值相等，即 det ( 1,2, , ) 1 A a 1 A1 a 2 A2 a A a A i n n j  i i  i i  in in  ij ij    推论 若行列式的某行元素全为零，则行列式的值为零。 例1 计算行列式 1 3 4 3 0 2 0 0 5 1 3 2 6 1 0 0    D  解：按第二行展开 1 4 3 5 3 2 6 0 0 2( 1) 3 2      D 4 3 3 2 2 6      12

ajiainai2a22a2n例2计算n阶上三角行列式行列式D.=ann解：可按第n行展开ala12ain-a22a2n-1D, =(-1)"+" ann= annDn- =amman-In-Dn-2 =annan-In-1"..al1a,-1n-1 In-1=a,a22"".anm

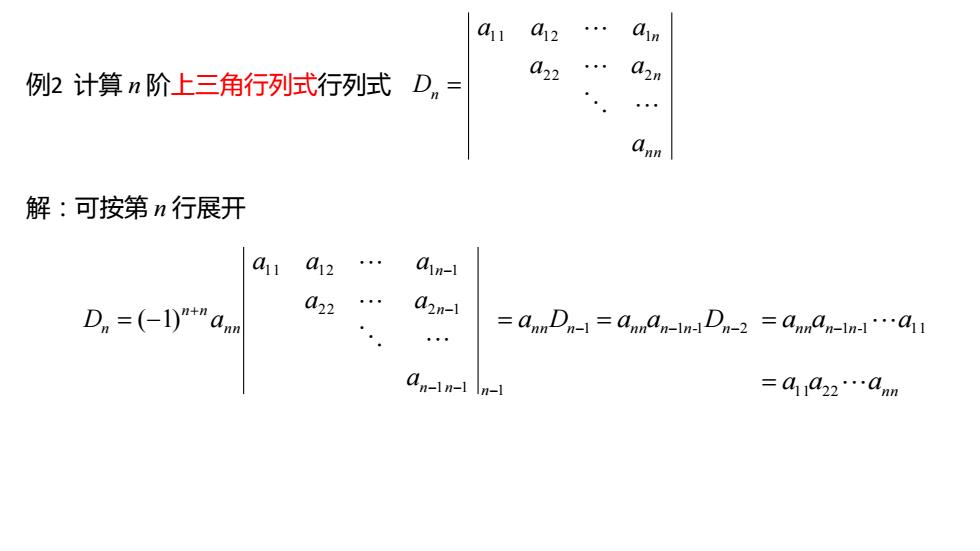
例2 计算 n 阶上三角行列式行列式 2 2 2 1 1 1 2 1 n n n n n a a a a a a D      解：可按第 n 行展开 1 1 1 2 2 2 1 1 1 1 2 1 1 ( 1)         n n n n n n n n n n a a a a a a D a      annDn1  annan1n-1 Dn2  annan1n-1 a11  a11a22 ann

性质2若n阶行列式的某两行元素对应相等，则行列式的值为零。用数学归纳法证明：当n=2时，由对角线展开法，结论显然成立；假设当n=k（k≥3)时，结论成立，即ais=αis(i±j;s=l,2,",n)且Dk=0令n=k+1，D，按第k+1行展开,则Dk+1=ak+11Ak+1+ak+12Ak+12+..+ak+1k+1Ak+1k+其中Ak+11Ak+12",A4k+1k+都是k阶行列式，且第i行与第j行元素对应相等由假设可知Ak+11=Ak+12=…=Ak+1k+1=0,故Dk+=0证毕

性质2 若 n 阶行列式的某两行元素对应相等，则行列式的值为零。 用数学归纳法证明： 当 n  2 时，由对角线展开法，结论显然成立； 假设当 n  k (k  3) 时，结论成立，即 ais  ajs (i  j;s 1,2,  ,n) 且 Dk  0 令 n  k 1 ， Dn 按第 k+1 行展开, 则 Dk1  ak11 Ak1 1  ak1 2Ak1 2  ak1k1 Ak1k1 其中 Ak1 1, Ak1 2,  , Ak1k1 都是 k 阶行列式，且第 i 行与第 j 行元素对应相等 由假设可知 Ak1 1  Ak1 2  Ak1k1  0 ，故 Dk1  0 证毕

性质3（可加性）aiai2danla12a12dinaua11Dbi2b5bin.b,z2 + Ci2a+cu+CinC+Ci2Ciinin1annanlan2anian2annanlan2ann证明：将左端行列式按第i行展开，得D=(bi +c)A, +(bi2 + C2)A2 +...+(bm +Cm)A=(b,Ai +bi2A2 +...+ bimAn)+(CiA1 +Ci2A2 +...+CinAm)= D, + D2证毕

性质3 （可加性） 1 2 1 1 2 2 1 1 1 2 1 n n n n i i i i in in n a a a b c b c b c a a a               1 2 1 2 1 1 1 2 1 1 2 1 2 1 1 1 2 1 n n n n i i in n n n n n i i in n a a a c c c a a a a a a b b b a a a                         证明：将左端行列式按第 i 行展开，得 i i i i i i in in Ain D (b c )A (b c )A (b c )  1  1 1  2  2 2   ( ) ( ) i1 i1 i2 i2 in in i1 i1 i2 i2 inAin  b A b A b A  c A c A c  D1  D2 证毕

2312312例356445693+ 62 +551+ 4733121265454+6=0+0=0312456观察：与矩阵加法的区别？新时代大学数学乐列教材

新时代大学数学系列教材 例3 观察 ：与矩阵加法的区别 ？ 1 2 3 456 579 1 2 3 4 5 6 1 4 2 5 3 6     1 2 3 1 2 3 4 5 6 4 5 6 1 2 3 4 5 6      0 0 0