《线性代数》课程教学资源（讲稿B，高教版）第三章 n维向量空间 3-2 向量组的线性相关性

向量组的线性相关性3-2引入(2, 1,-3, 0)021-31°矩阵的行向量组(-1,1, 3, 2)32-11(1, 2, 0, 2)2120量8, = (1, 0, 0), 82 =(0, 1, 0), c, =(0, 0, 1)2°在3维向量空间R3中，三个坐标向量任一向量α=(,）都可以表示为α=3°线性方程组α+α+

3-2 向量组的线性相关性 引入 1°矩阵 的行向量组             1 2 0 2 1 1 3 2 2 1 3 0 2°在3维向量空间 R 3 中，三个坐标向量 1, 0, 0, 0,1, 0, 0, 0,1  1   2   3  任一向量   (a1 ,a2 ,a3 ) 都可以表示为 1 1 2 2 3 3   a   a   a  3°线性方程组                1 1 3 1 2 1 1 0 1 2 1 4 1 2 3 1 2 3 1 2 3 x x x x x x x x x (1, 2, 0, 2) ( 1,1, 3, 2) (2, 1, 3, 0)   1  2  3  b

一、向量组的线性组合定义1给定向量组αiα2,αmβ，若存在一组数k,kz,km，使得β=k,a,+k,a,+..+kmam则称向量β是向量组α,α2αm的线性组合，或称向量β可由向量组α,α2,αm线性表示。所有αi,α2,,αm的线性组合的集合用L(αi,α2，,αm)表示。例如,向量组α,=(2,1,-3,0)，α2=(-1,1,3,2)，β=(1,2,0,2)因为β=α,+αz，所以β是αi,α,的线性组合。注1°零向量是任一向量组的线性组合。2°向量组α1,α2，"",αm中任一向量都可由这个向量组线性表示α, =0αf +.+0α,- +lα, +0αi++ +..+0αm3°R"=L(,82,"",8n)

定义1 给定向量组 1 ,2 ,  , m , ，若存在一组数 ，使得 一、向量组的线性组合 m k , k , , k 1 2  m m   k1 1  k2 2  k  则称向量 是向量组 的线性组合，或称向量 可由向量组 线性表示。所有 的线性组合的集合用 表示。     m , , , 1 2      m , , , 1 2     m , , , 1 2  ( , , , ) L 1 2   m (2, 1, 3, 0) ( 1,1, 3, 2) (1, 2, 0, 2) 例如，向量组 1   ，2   ，  因为  1 2 ，所以  是 1 ,2 的线性组合。 注 1° 零向量是任一向量组的线性组合。 3° R ( , , , ) 1 2 n L n     2° 向量组 1 ,2 ,  , m 中任一向量都可由这个向量组线性表示。 1 1 1 0 0 1 0 0 .       i i i i m         

R" = L(),62,"",8n),（o)1000001即，任一n维向量均可由Sj,&2,8线性表出。(,X2,.,Xn)= XG +X282 +..+Xnn设αj, α2, .., αm ER", 则 L(αi,α2, .., αm) 为 R"的一个子空间——由αi，αz，…，αm生成的子空间

即，任一n维向量均可由 线性表出. 设1 , 2 , ., m Rn , 则 L(1 ,2 , ., m) 为 Rn 的一 个子空间——由1 , 2 , ., m 生成的子空间. 1 2 1 2 ( , , , ), 1 0 0 0 1 0 , , , . 0 0 1 n n n L                                               R 1 2 , , , n    1 2 1 1 2 2 ( , , , ) . n n n x x x x x x       

线性方程组的向量表示a11xi+a12x2+.bi,ainna21xi+a22x2+..+a2nXn=b2bmaml.i+am2x2+.+Hamxn=-axBax+aαi+XiA = (αi, α2, ..., an)

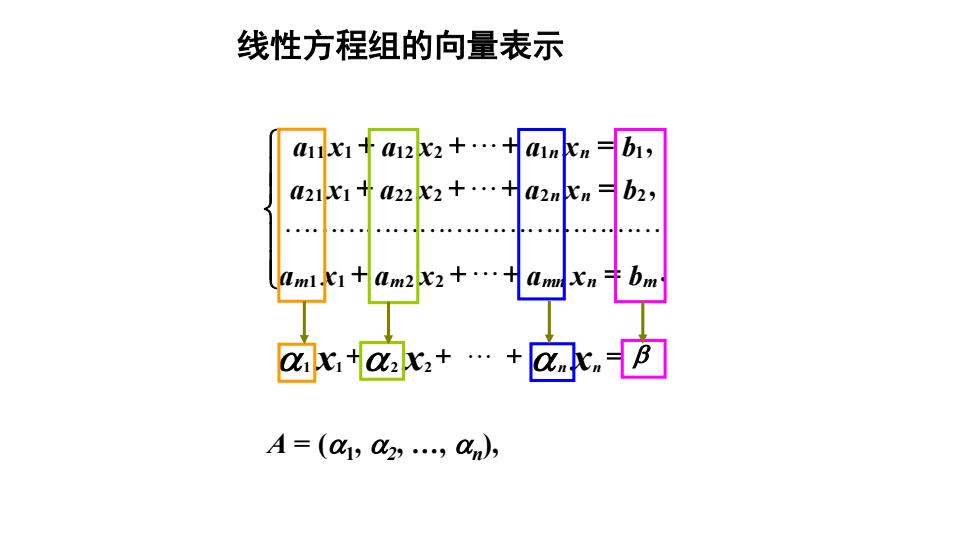
    1 1 2 2 x  x   x   n n 线性方程组的向量表示                    . , , 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 a x a x a x b a x a x a x b a x a x a x b m m mn n m n n n n     A = (1 , 2 , ., n )

定理1设A=(αi,α2,……，αn),则下列命题等价：10 b e L(α1, α2, ..., αn);2° AX=b有解;30 R(A)= R(A)( 或R(A:b)= R(A)证1°≤2°: beL(αj, α2,..., αn)有数x, X2, .. Xn使得 xa+xα,++x,α,=bXixX2X(αi,α2,",αn)=b,AX=b有解X=x

定理1 设 A = (1 , 2 , ., n ), 则下列命题等价： 1 o b  L(1 , 2 , ., n ); 2 o AX = b有解; 3 o 证 1 o 2 o：bL(1 , 2 , ., n ) 有数 x1 , x2 , ., xn 使得 R A R A A b R A ( ) ( ). R )   （或     1 1 2 2 , n n x x x b        1 2 . n x x AX b X x               有解 1 2 1 2 ( , , , ) , n n x x b x                