《线性代数》课程教学资源（讲稿B，高教版）第二章 行列式 2-1 n阶行列式的定义

第二章行列式2-1n阶行列式的定义2-2行列式的性质和计算2-3拉普拉斯定理2-4克拉默法则2-5矩阵的秩

第二章 行列式 2-1 n 阶行列式的定义 2-2 行列式的性质和计算 2-3 拉普拉斯定理 2-4 克拉默法则 2-5 矩阵的秩

2-1n阶行列式的定义aiix +ai2x, =b考虑二元线性方程组[a2 +a22x =b,b,a22 -ai2b2xa22-a221当aa22一za±0时，则方程组的解为a,bz -b,a21X2ai22 -ai221b,hd12aa12d记矩阵A：Ab,ba22a21a21a-01ai1a12称为一个二阶行列式，且aα22-ai221= det A=Aa22a21a22[a21

2-1 n 阶行列式的定义        2 1 1 2 2 2 2 1 1 1 1 2 2 1 a x a x b a x a x b 考虑二元线性方程组 当 a1 1a2 2 a1 2a2 1  0 时，则方程组的解为              1 1 2 2 1 2 2 1 1 1 2 1 2 1 2 1 1 2 2 1 2 2 1 1 2 2 1 2 2 1 a a a a a b b a x a a a a b a a b x 记矩阵 21 22 11 12 a a a a                            2 1 2 1 1 1 2 2 2 2 1 1 2 1 2 1 2 2 1 1 1 2 , , a b a b A b a b a A a a a a A 称 为一个二阶行列式，且 a a a a A a a a a det 1 1 2 2 1 2 2 1 2 1 2 2 1 1 1 2     A

ax +a12X2 = b的解可记为当detA±0时，二元线性方程组[a21)+a22x2=b,ba2bdet A,a22xdet Aa12aa21b,aib2det A,a21X2det Aa2aila22a21

当 时，二元线性方程组 的解可记为        2 1 1 2 2 2 2 1 1 1 1 2 2 1 a x a x b a x a x b det A  0                  A A a a a a a b a b x A A a a a a b a b a x det det det det 2 2 1 2 2 1 1 1 2 2 1 2 1 1 1 2 1 2 1 2 2 1 1 1 2 2 2 2 1 1 2 1

二阶行列式定义由四个数排成二行二列（横排称行、竖排称列）的数表aual2a21(22数[aia22 -a12a21称为数表所确定的二阶行列式，记为aii a2[a21 a22

由四个数排成二行二列（横排称行、竖排称列） 的数表 数 a a a a 11 22 12 21  称为数表所确定的 二阶行列式, 记为 11 12 21 22 a a a a 二阶行列式定义 11 12 21 22 a a a a

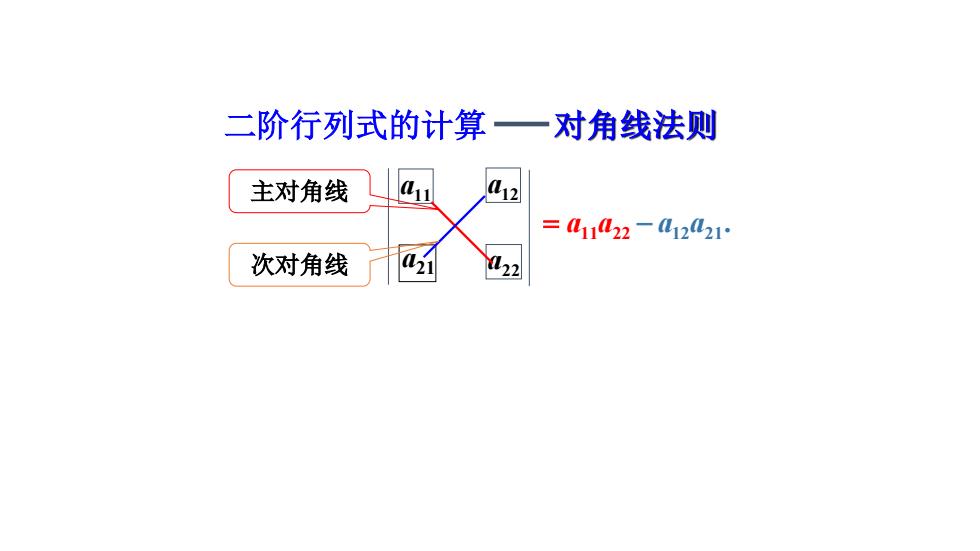
二阶行列式的计算一对角线法则a主对角线2=a1a22-(1221a21次对角线22

a21 11 a 12 a 22 a 主对角线 次对角线 对角线法则 11 22  a a . 12 21  a a 二阶行列式的计算